Предмет: Алгебра,
автор: psvetlana200
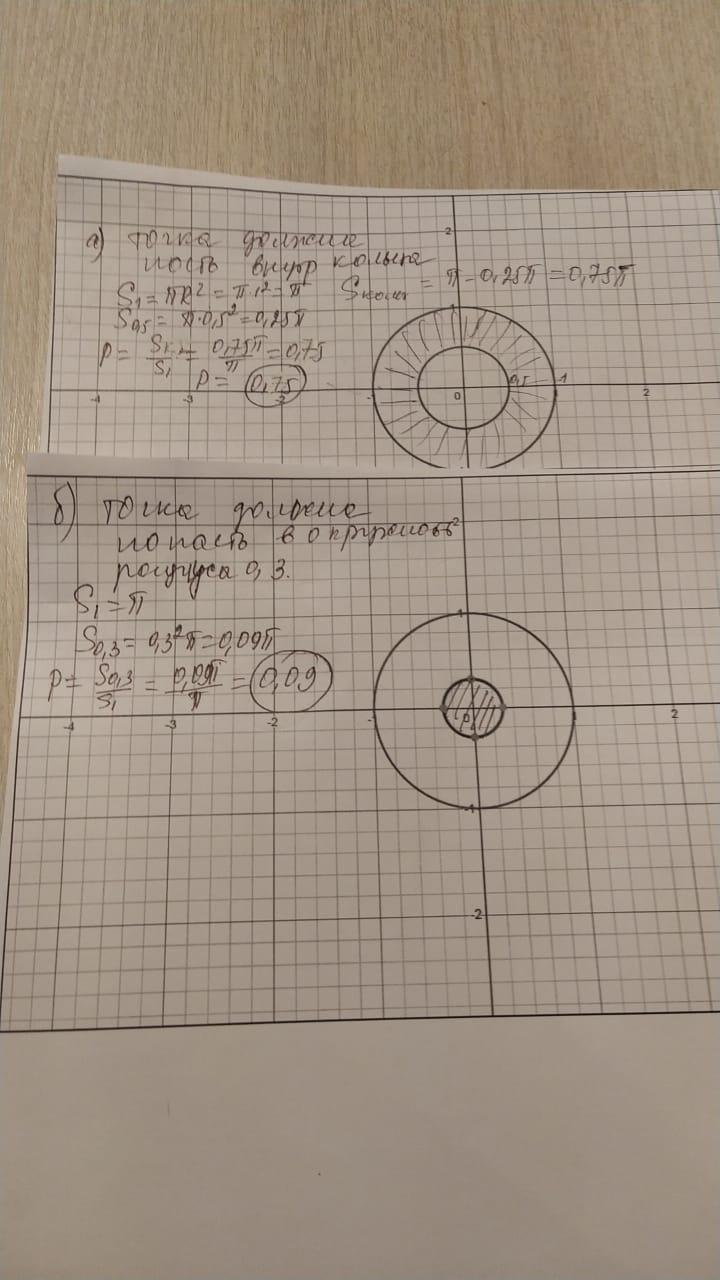
В кругу единичного радиуса с центром в точке (0,0) наугад выбирают точку. Какова вероятность того, что расстояние от данной точки до центра окружности
а) более 0,5; б) меньше 0,3.
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
Решаем, используя геометрическое определение вероятности
S○=pi×R^2, где R=1 → S○=pi
а) более, ето строгое >
Рассмотрим точки , которие рассположени до 0,5.
удовлетворяют точки, расположенние от центра на растояниии от 0 до 0.5
r=0.5
S●=pi×(r)^2=0.5^2 pi=0.25рі
P=S●/S○=0.25pi/pi=0.25
Тогда искомая вероятнось
Р(растояние> 0,5)=1-0.25=0.75
б) рассмотрим точки, которие удалени на 0.3 и больше. необходимие точки находятся в круге с радиусом от 0.3 до 1.
Поетому S●=pi×(R^2-r^2)=(1-0.09)pi=0.91рі
P=0.91pi/pi=0.91
Поетому
Р(растояние <0.3)=1-0.91=0.09
Автор ответа:
1
Ответ: приложен
Объяснение:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: LeraZenart
Предмет: Русский язык,
автор: Vika02112004
Предмет: Русский язык,
автор: alikamola
Предмет: Математика,
автор: Bella1001
Предмет: Математика,
автор: jafarjafar2007