Предмет: Математика,
автор: Klencnc17
Нужно решить, пошагово
Приложения:
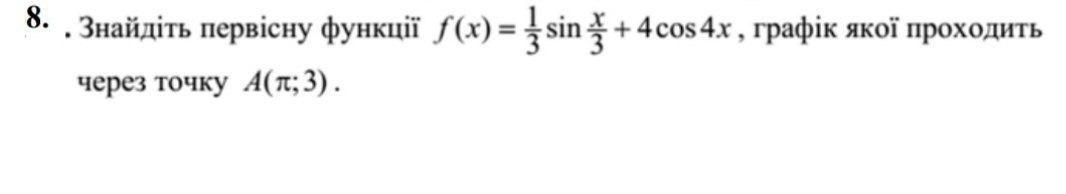
Ответы
Автор ответа:
0
Ответ:
- общее решение
Подставим координаты точки А
х = П
у = 3
Похожие вопросы
Предмет: Русский язык,
автор: светлана11124
Предмет: Русский язык,
автор: Саша200518
Предмет: Окружающий мир,
автор: belekesch
Предмет: Английский язык,
автор: SevkaBurka
Предмет: Математика,
автор: Фз206207