Предмет: Алгебра,
автор: PICPRO
Решить тригонометрческие уравнения на фото
Приложения:
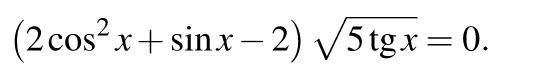
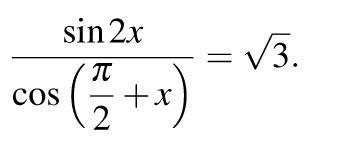
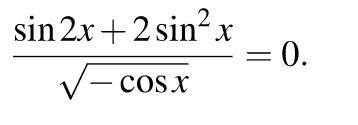
Ответы
Автор ответа:
0
1.
Ограниченте на тангенс:
Тангенс неотрицателен когда его аргумент лежит в 1 и 3 четвертях, значит и корни исходного уравнения дрожи сдесь лежать:
2.
ОДЗ:
Похожие вопросы
Предмет: Английский язык,
автор: tutyumova
Предмет: Русский язык,
автор: megaievghienii
Предмет: Қазақ тiлi,
автор: Джесика2002
Предмет: Математика,
автор: karina557799