Предмет: Алгебра,
автор: PICPRO
Решить тригонометрческие уравнения на фото
Приложения:

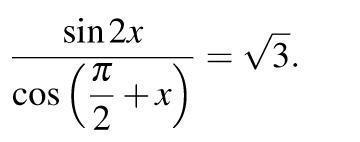
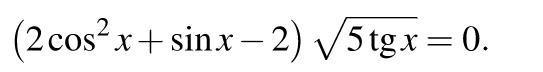
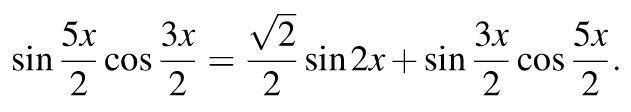
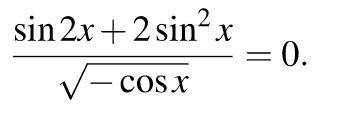
Ответы
Автор ответа:
1
ОДЗ:
Так как точки типа не входят в ОДЗ, то первый корень не есть решение. Тогда ответом есть:
2. Второе задание уже решено (см. в профиле).
Похожие вопросы
Предмет: Окружающий мир,
автор: krasopetka2
Предмет: Другие предметы,
автор: olgaklanatko7
Предмет: Русский язык,
автор: ruslan188
Предмет: Математика,
автор: Huzuca