Question

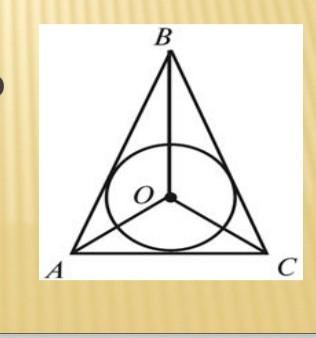
у трикутник ABC, (АВ=ВС) вписане коло з центром О, доведіть що трикутник АОС рівнобедрений​

Answer 1

В равнобедренном треугольнике углы при основании равны (признак и свойство).

△ABC - равнобедренный => ∠BAC=∠BCA

Центр вписанной окружности (O) - пересечение биссектрис.

AO, CO - биссектрисы.

Биссектриса делит угол пополам.

∠OAC=∠BAC/2, ∠OCA=∠BCA/2 => ∠OAC=∠OCA

△AOC - равнобедренный (т.к углы при основании равны)