Предмет: Геометрия,
автор: 7695679thjkhgjkgh
ДАМ 35 БАЛЛОВ!!!!
Образующая конуса с основанием конуса образует угол 60° градусов, а длина окружности равна 20 . Найдите площадь конуса и его объём
. Найдите площадь конуса и его объём
Ответы
Автор ответа:
0
Ответ:
Розв'язок до завдання на фото. Якщо щось не зрозуміло, запитуй.
Приложения:
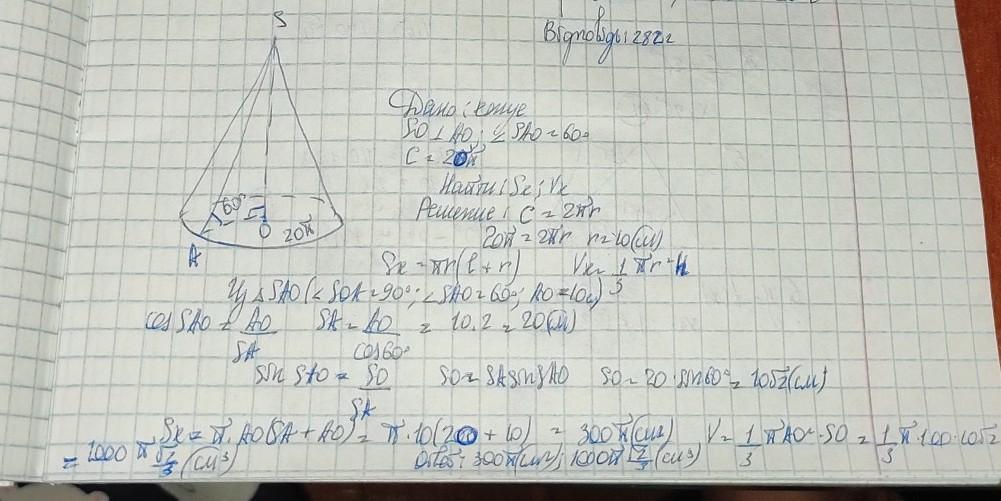
Автор ответа:
0
Ответ:
Sполн=100π
Vкон= 1000π/√3
Объяснение:
Дано: конус-Sr
l=20π;. <A=60
S,. V,
Sполн=Sосн+Sбок.
Sосн = πr^2;. Sбок =1/2*2πr*L
Vkon = 1/3*Sосн*h
h= r√3= √3/2π*l
Если угол образующей конуса (L) и плоскость основания (.r-радиус основания) составляет 60°, то L=2r
r = l/2π
L= 2* l/2π = l/π
Sбок = 1/2*l*l / π = l^2 : 4π
Sосн = π*(l/2π)^2= l^2 : 4π
Sполн = l^2 : 2π
Vкон=1/3*l^2/4π*√3/2π*l
Vкон = √3/(24π^2)*l^3
подставляем данные
Sполн= ( 20π)^2:2π= =100π
Vkon =√3/(24π^2) *(20π)^3 =1000π/√3
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: IINepoNII
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Карина6751
Предмет: Русский язык,
автор: катя5321