Question

Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.

Answer 1

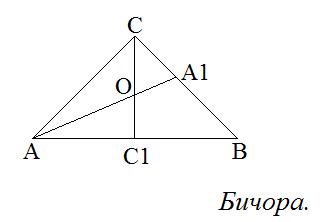
Чертеж во вложении.
1) Проведем высоту СС1 к основанию АВ и биссектрису АА1 к боковой стороне ВС.
2) Расмотрим треугольник АСС1. Пусть на одну часть приходится х см, тогда АС1=2х (высота равнобедр тр-ка, проведенная к оснвоанию является медианой) и АС=3х. СС1= 30 (по усл). По т. Пифагора
$(2x)^2+900=9x^2$
$4x^2+900=9x^2$
$5x^2=900$
$x= sqrt{180}$
$x=6 sqrt{5}$ , то есть на одну часть приходится $6 sqrt{5}$ см.
Значит, $AC=3* 6sqrt{5}=18 sqrt{5}$ см
$AC1=2*6 sqrt{5}=12 sqrt{5}$ см
3) Так как СС1- высота, АА1- биссектриса и АС=ВС, то $frac{AC}{CO}= frac{AC1}{OC1}$
Пусть ОС1=х, тогда т.к. СС1=30, СО=30-х. Подставим в пропроцию:
$frac{18 sqrt{5} }{30-x}= frac{12 sqrt{5} }{x}$
$x 18sqrt{5}=12 sqrt{5} (30-x)$ 
Разделим на $6 sqrt{5}$ :
$3x=2(30-x)$
$3x+2x=60$
5x=60
x=12, то есть ОС1= 12 см.
Тогда ОС=30-12=18 см.
Ответ: 12 см, 18 см.