Предмет: Геометрия,
автор: nKrynka
Помогите, пожалуйста, решить задачу:
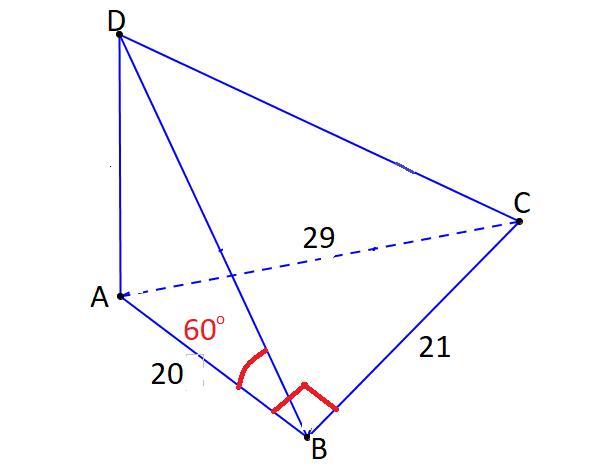
Основанием пирамиды является треугольник ABC, стороны которого АВ = 20 см, АС-29 см, ВС = 21 см. Грани DAB и DAC перпендикулярны к основанию, а грань DBC образует с ней угол 60". Найдите площадь боковой поверхности пирамиды.
( с полным объяснением и рисунком, пожалуйста)
Ответы
Автор ответа:
1
Заданы стороны треугольника ABC: АВ = 20 см, АС = 29 см, ВС = 21 см.
По квадратам сторон видим, что треугольник прямоугольный.
Угол В прямой, угол АВД является плоским углом между основанием АВС и боковой гранью ВСД.
Высота к основанию АД = АВ*tg 60° = 20√3 см.
Высота ВД = АВ/cos 60° = 20/(1/2) = 40 см.
Теперь находим площади боковых граней.
S(ABD) = (1/2)*20*20√3 = 200√3 см².
S(ABD) = (1/2)*29*20√3 = 290√3 см².
S(BCD) = (1/2)*40*21 = 420 см².
Ответ: Sбок = 200√3 + 290√3+ 420 = (490√3 + 420) см².
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zirma78
Предмет: Русский язык,
автор: narmin123
Предмет: Русский язык,
автор: 198718
Предмет: Математика,
автор: alexeikot456