Предмет: Алгебра,
автор: reitergalina2005
Номер 4.143.............
Приложения:
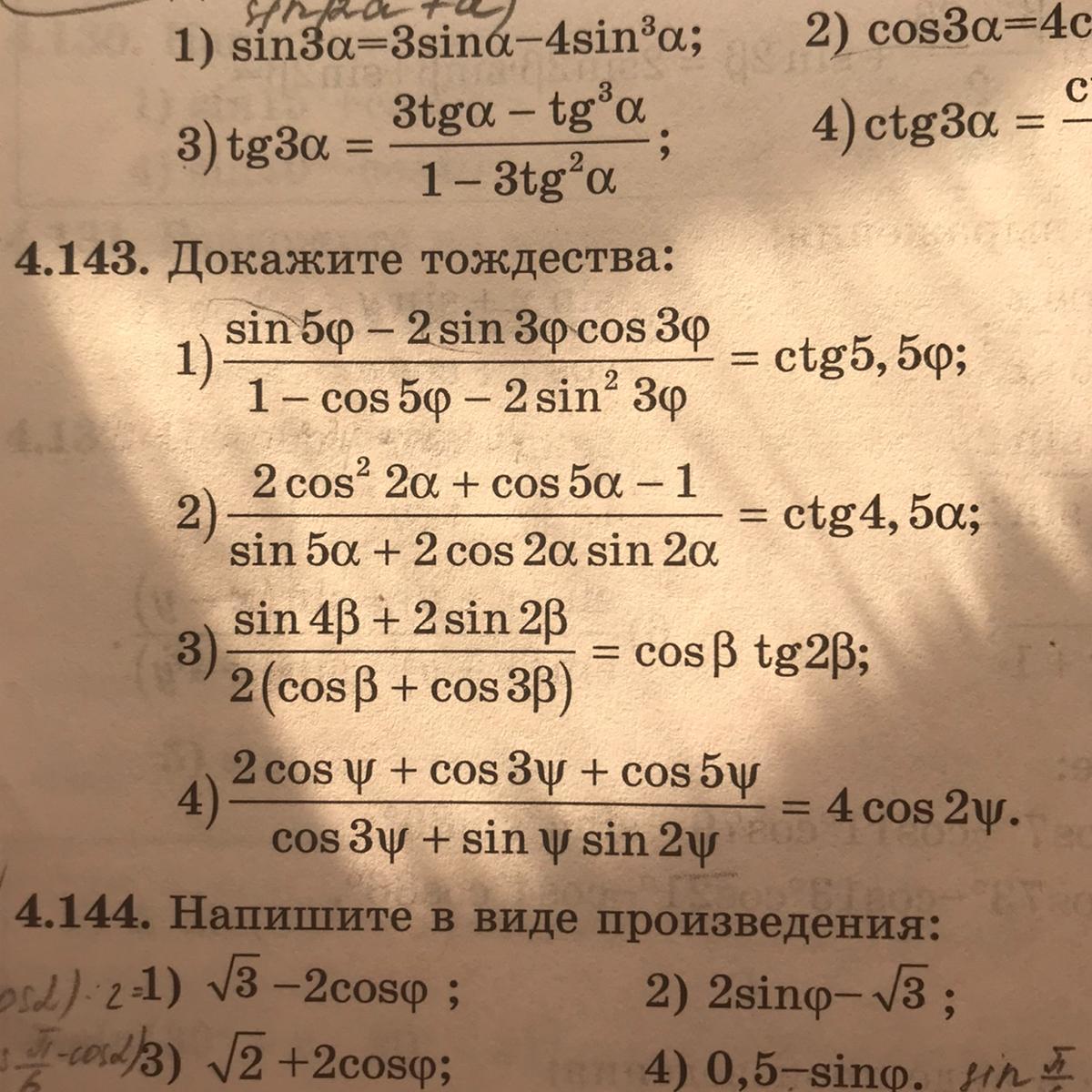
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
1)
Приведемм отдельно числитель и знаменатель
2sin3acos3a=sin6a
sin5a-sin6a=2cos5.5a sin(-a/2)
1-cos5a-2sin^2 3a= cos6a-cos5a= -2sin5.5a sin(a/2)
Тогда имеем
-2cos5.5a sin(a/2)/(-2sin5.5a sin(a/2))= cos5.5a/sin5.5a=ctg5.5a
2)
cos5a+cos4a=2cos(4.5a) cos (a/2)
sin5a+sin4a=2sin4.5a cos(a/2)
2cos(4.5a) cos (a/2)/(2sin4.5a cos(a/2))= cos4.5a/sin4.5a=ctg4.5a
3)
sin4b+2sin2b=2sin2b(cos2b+1)
cos2b=2cos^2b-1 → 2sin2b(cos2b+1)=2sin2b×cos^2b
cosb+cos3b=2cos2b cos(-b)
4sin2b×cos^2b/(4cos2b cosb)=tg2b×cosb
4)
2cosa+cos3a+cos5a=(cosa+cos3a)+(cosa+cos5a)=
2cos2a×cosa+2cos3a×cos2a=2cos2a(cosa+cos3a)
cos3a+sina×sin2a=cos3a+1/2(cosa-cos3a)= 1/2(cosa+cos3a)
2cos2a(cosa+cos3a)/(1/2(cosa+cos3a))=4cos2a
reitergalina2005:
Огромнооое спасибо❤️
:)
Похожие вопросы
Предмет: Русский язык,
автор: Ter123454
Предмет: Українська література,
автор: lidabm
Предмет: Русский язык,
автор: loginloginlog
Предмет: Информатика,
автор: annever05
Предмет: Английский язык,
автор: никкккка6