Question

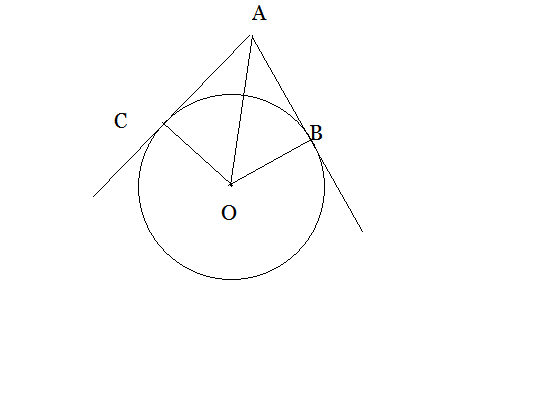
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60° , а расстояние от точки А до точки О равно 6. 

Answer 1

Радиусы окружности, проведенные в точку касания-перпендикуляры ⇒
ΔАСО и ΔАВО-прямоугольные
АО-общая
СО=ОВ(как радиусы)
АС=АВ(как отрезки касательных, проведенных из одной точки)
ΔАСО=ΔАВО ⇒
углы САО и ОАВ тоже равны=60/2=30
катет, лежащий против угла в 30 градусов равен 1/2 гипотенузы, значит ОС или ОВ=АО/2=6/2=3