Question

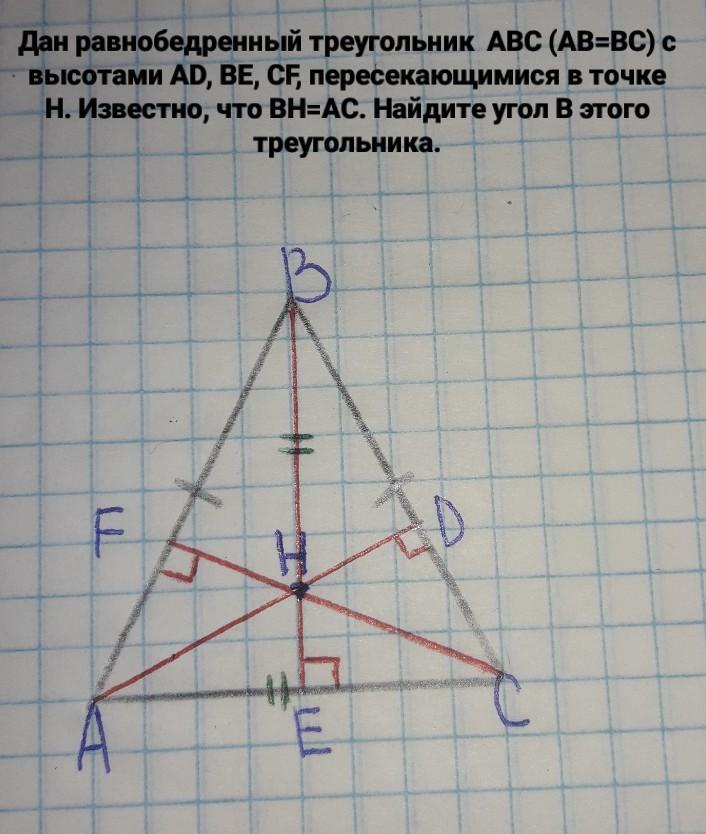
решить задачу........​

Answer 1

Пусть О - центр описанной окружности, тогда угол АОС=2В, АОЕ=В;

ОЕ=АЕ·ctg B. Как известно, ВН=2ОЕ (почему это так, доказывать здесь не буду - образованный школьник обязан это знать), поэтому ВН=АС·ctg B. Но по условию ВН=АС⇒ctg B=1; B=45°.

Ответ: 45°

Замечание. Эта задача дает неожиданный пример четырехугольника с тремя равными углами и равными диагоналями, не являющимся прямоугольником. На приведенном чертеже это четырехугольник АВСН - у него углы А, В и С равны 45°, а диагоналями являются отрезки АС и ВН. Правда, этот четырехугольник не является выпуклым, ну и что - он не перестает быть четырехугольником.