Предмет: Математика,
автор: Аноним
Помогите пожалуйста
Приложения:
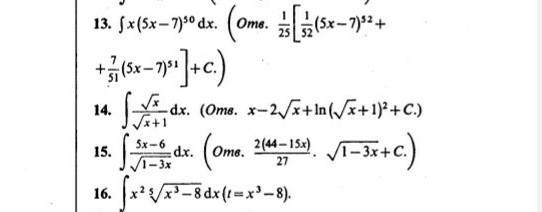
Ответы
Автор ответа:
2
Ответ:
13.
14.
15.
16.
Похожие вопросы
Предмет: Русский язык,
автор: mari2404
Предмет: Русский язык,
автор: nuriknav
Предмет: Английский язык,
автор: бином2
Предмет: Физика,
автор: johnnypechersk
Предмет: Математика,
автор: Аноним