Question

Помогите, пожалуйста, решить задачу:
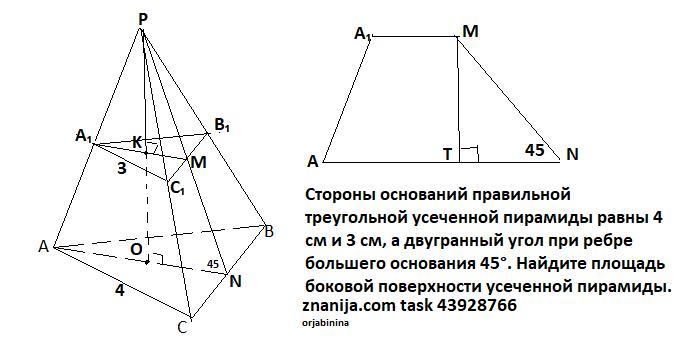
Стороны оснований правильной треугольной усеченной пирамиды равны 4 см и 3 см, а двугранный угол при ребре большего основания-45°. Найдите площадь боковой поверхности усеченной пирамиды. ( с полным объяснением и рисунком, пожалуйста)

Answer 1

Стороны оснований правильной треугольной усеченной пирамиды равны 4 см и 3 см, а двугранный угол при ребре большего основания 45°. Найдите площадь боковой поверхности усеченной пирамиды.

Объяснение:

Пусть  ABCA₁B₁C₁  данная  пирамида . Пусть M середина ребра B₁C₁  , N середина  BC  ⇒ AN⊥BC , тк медиана в равностороннем треугольнике является высотой. По т. о трех перпендикулярах MN⊥ВС, поэтому двугранным углом  при ребре большего основания , будет

угол ∠АNМ =45°.

Боковые грани равные равнобедренные трапеции ,

S(бок) =3*S(трапеции) ,  S(трапеции) =h* (a+b)/2, где h-апофема

Найдем в равносторонних ΔАВС, ΔА₁В₁С₁ радиусы вписанных окружностей r =$\frac{a_3\sqrt{3} }{6}$.  Получим r(АВС)=$\frac{2\sqrt{3} }{3}$  см ,   r(А₁В₁С₁)=$\frac{\sqrt{3} }{2}$ см.

1)ΔONP- прямоугольный , ∠АNМ =45°  ⇒ равнобедренный и РО= ОН =$\frac{2\sqrt{3} }{3}$  см

2) ΔРКМ подобен ΔРОN по 2-м углам :∠Р-общий , ∠ONP=∠KMP как соответственные , значит  $\frac{r_1}{r} =\frac{PK}{PO}$  , $\frac{\frac{\sqrt{3} }{2} }{r} =\frac{PK}{r}$   , PK=$\frac{\sqrt{3} }{2}$ см.

3) КО=РО-РК= =$\frac{\sqrt{3} }{2}$ см.

4)Пусть в А А₁MN- трапеции МТ⊥АN  , тогда высота  МТ=КО=$\frac{\sqrt{3} }{2}$ см , ∠АNМ =45° . Для ΔТМN-прямоугольного sin45°=$\frac{MT}{MN}$ , MN=$\frac{\sqrt{3} }{2} *\frac{2}{\sqrt{3} } =\frac{\sqrt{6} }{6}$ (cм).

5)S(бок) =3*h* (a+b)/2=  $3*\frac{\sqrt{6} }{6} *\frac{3+4}{2}$  = $\frac{7\sqrt{6} }{4}$  (см²).