Предмет: Алгебра,
автор: buneevaela
Вычислить площадь фигуры огранниченной интегралами :
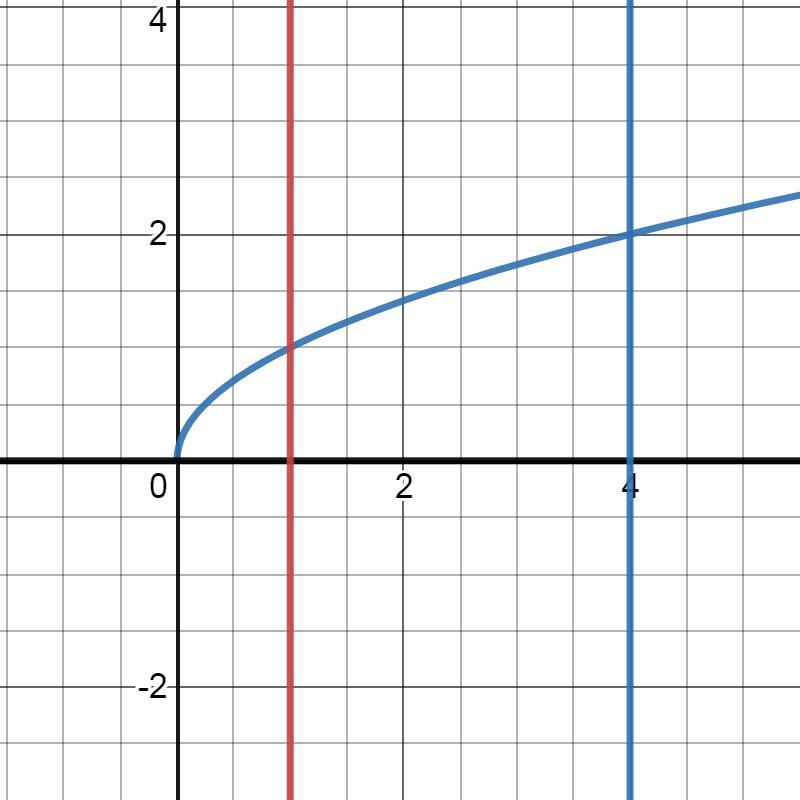
y=√x
x=1, x=4 , y=0
СРОЧНО
buneevaela:
Там не интегралами а линиями
Ответы
Автор ответа:
1
Объяснение:
Ответ: S=4,66667 кв. ед.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: belonojkoanna21
Предмет: Русский язык,
автор: geny2007
Предмет: Геометрия,
автор: Просто100так