Предмет: Математика,
автор: leonecor7
Три задания по функциям. 50 баллов + 50 за лучший
Приложения:
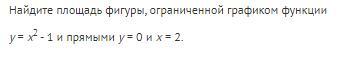
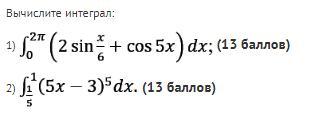

Ответы
Автор ответа:
1
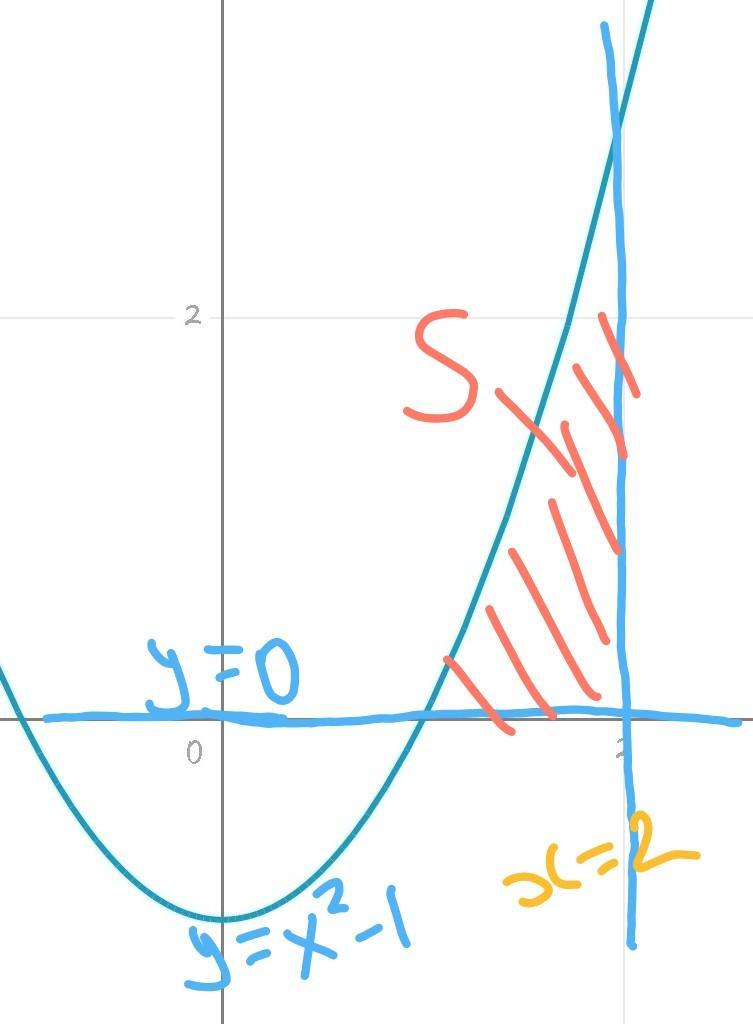
1.
2.
1)
2)
3.
1)
2)
Приложения:
leonecor7:
Премного благодарен. Не могли бы вы помочь еще с 2-мя заданиями? Тоже за 50 баллов
Похожие вопросы
Предмет: Английский язык,
автор: 2007Никита
Предмет: Русский язык,
автор: anzhelaantropo
Предмет: Окружающий мир,
автор: torikoza
Предмет: Информатика,
автор: khkhara