Предмет: Геометрия,
автор: LucDr
Найдите периметр прямоугольника, если его площать равна 272, а отношение соседних сторон равно 4:17.
Ответы
Автор ответа:
0
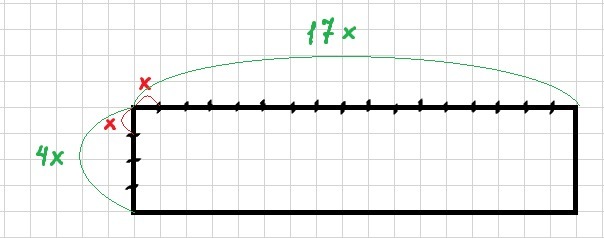
Отношение 4:17 означает, что 4 равных части одной стороны относятся к 17 таким же равным частям другой стороны.
Обозначим одну такую часть через х (смотри рисунок).
Тогда длина одной стороны будет 4х.
Длина второй стороны (смежной) будет 17х.
Площадь прямоугольника - произведение двух смежных сторон. Она известна: 272. Составим уравнение и найдем х, т.е. длину одной части.
4х*17х=272
68х²=272
х²=272:68
х²=4
х=√4
х=2
Длина одной части равна 2.
Значит длина одной стороны: 4х=4*2 = 8.
Длина второй стороны: 17х=17*2=34.
Периметр прямоугольника - сумма длин всех сторон.
Р= 8+8+34+34 = 84
Ответ: 84.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Elvin711
Предмет: Английский язык,
автор: t0569691
Предмет: Математика,
автор: liminavaliza96
Предмет: Химия,
автор: Andrew1997