Предмет: Математика,
автор: kyy02
решить неравенство.......
Приложения:
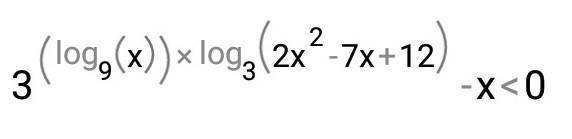
Ответы
Автор ответа:
2
ОДЗ:
Заметим, что равносильность справедлива на ОДЗ. При этом мы использовали то, что 3>1. В общем виде использованные равносильности основаны на следующем факте:
знак выражения совпадает на ОДЗ со знаком выражения
Учитывая ОДЗ, получаем ответ:
Похожие вопросы
Предмет: Русский язык,
автор: пов1
Предмет: Окружающий мир,
автор: MixBobrov12359
Предмет: Русский язык,
автор: Kettekat2002
Предмет: Биология,
автор: 1Лерапард1
Предмет: Биология,
автор: умница121212