Предмет: Математика,
автор: MolkyWay
ПОМОГИТЕ!!!!! ОЧЕНЬ НУЖНО!!!
Приложения:

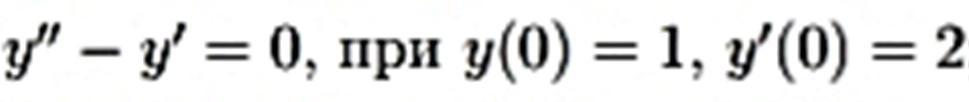
Ответы
Автор ответа:
2
Ответ:
везде замена
1.
общее решение
2.
общее решение
частное решение
3.
общее решение
частное решение
Похожие вопросы
Предмет: Русский язык,
автор: ppp0197622
Предмет: Окружающий мир,
автор: swemlana
Предмет: Английский язык,
автор: sasha252
Предмет: Математика,
автор: Zera10Mysaeva
Предмет: Русский язык,
автор: cat571