Question

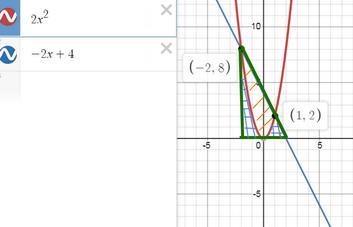
Найти, объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью абcцисс: y=2x^2, y= -2x+4

Answer 1

Ответ:

Пошаговое объяснение:

$\displaystyle V=\pi \int\limits^1_{-2} {\bigg ((-2x+4)^2-(2x^2)^2} \bigg )\, dx =\int\limits^1_{-2} {(4x^2-16x+16-4x^4)x} \, dx =$

$\displaystyle =\pi \bigg (\frac{4x^3}{3} \bigg |_{-2}^1-8x^2\bigg |_{-2}^1-16x\bigg |_{-2}^1-4\frac{x^5}{5} \bigg |_{-2}^1 \bigg )=\frac{288}{5} \pi$

мы взяли объем тела зеленого треугольника (конуса)  и вычли объем нейлоида (тело отмечено синими крестиками) и получили объем нужного тела (оранжевые линии)