Предмет: Математика,
автор: lorgends
Дифференциальное уравнение второго порядка! Помогите решить,пожалуйста,очень нужно.
Приложения:
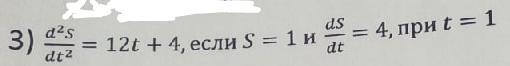
Ответы
Автор ответа:
0
Ответ:
общее решение
частное решение
Похожие вопросы
Предмет: Технология,
автор: Аноним
Предмет: Русский язык,
автор: btnbtn06
Предмет: Русский язык,
автор: никнэйм5
Предмет: Русский язык,
автор: vkhate
Предмет: Литература,
автор: A5D5E5L5I5N5A