Предмет: Математика,
автор: sashaizomska
решите интеграл
спасите,помогите
Приложения:
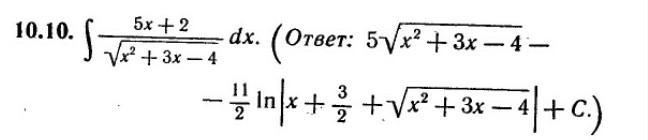
Ответы
Автор ответа:
1
Ответ:
В числителе делаем производную знаменателя: 2х+3
Похожие вопросы
Предмет: Английский язык,
автор: Виктор111111111111
Предмет: Русский язык,
автор: СпящийСЛОН
Предмет: Английский язык,
автор: Виктор111111111111
Предмет: Математика,
автор: evtpasha2017
Предмет: Литература,
автор: aborina2002