Предмет: Алгебра,
автор: treyarchin
Помогите с дифференцированием функции
Приложения:
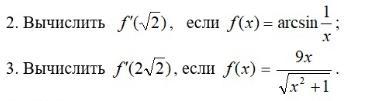
Ответы
Автор ответа:
1
Ответ:
2.
3
Похожие вопросы
Предмет: Русский язык,
автор: nenahu234234
Предмет: Русский язык,
автор: Adinka2002
Предмет: Английский язык,
автор: kuuyo9876
Предмет: Русский язык,
автор: esonne