Question

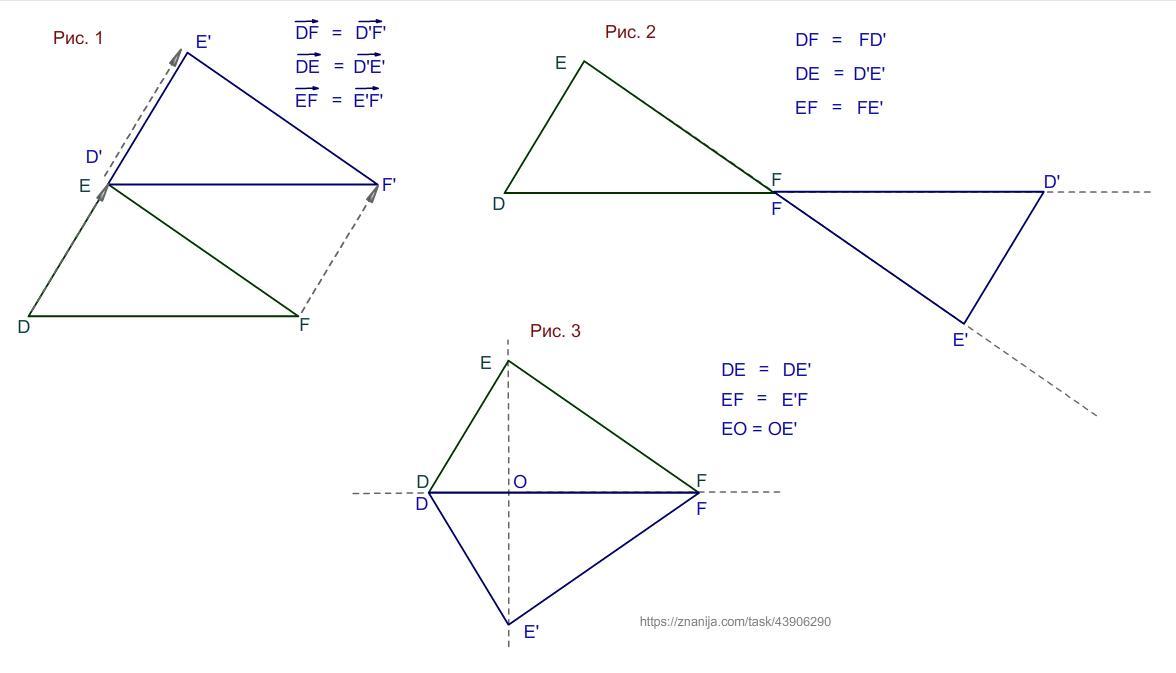
накресліть трикутник def побудуйте образ трикутника 1) при паралельному перенесенні на вектор DE 2) при симетрії відносно точки F 3) Від симетрії відносно прямої DF (((ПАМАГИТЕ СМПСИТЕ)))))

Answer 1

Ответ:

Приложен рисунок к выполненному заданию.

Объяснение:

Начертить треугольник DEF. Построить образ треугольника
1) при параллельном переносе на вектор DE;
2) при симметрии относительно точки F;
3) при симметрии относительно прямой DF.

Параллельным переносом на некоторый заданный вектор $\displaystyle \vec{a}$ называется такое отображение плоскости на саму себя, при котором каждая точка М плоскости переходит в такую точку М₁ той же плоскости, и выполняется равенство векторов $\displaystyle \overrightarrow{MM_{1}} = \vec{a}$

Рисунок 1.

1) Начертим треугольник DEF.  

Построим образ треугольника DEF при параллельном переносе на вектор $\displaystyle \overrightarrow{DE}$.

При параллельном переносе на вектор $\displaystyle \overrightarrow{DE}$
- точка Е отобразится на такую точку E', которая получается перемещением точки E на расстояние, равное длине вектора  $\displaystyle \overrightarrow{DE}$, в направлении, совпадающем с направлением вектора  $\displaystyle \overrightarrow{DE}$,

  $\displaystyle \overrightarrow{DE}=\overrightarrow{EE'},$

- точка D отобразится в точку D' такую, что точки D' и E совпадут, так как точка E является концом вектора $\overrightarrow{DE}$,

$\displaystyle \overrightarrow{DE} = \overrightarrow{DD'}$,

- точка F отобразится на такую точку F', такую, что

$\displaystyle \overrightarrow{DE}=\overrightarrow{FF'}$.

Соединим точки D'E'F'.

Треугольник  D'E'F' является образом треугольника DEF при параллельном переносе на вектор  $\displaystyle \overrightarrow{DE}$.

• Центральной симметрией называется симметрия относительно точки.
• Центр симметрии фигуры, это точка, относительно которой для любой точки фигуры найдется симметричная ей точка, также принадлежащая данной фигуре.

Рисунок 2.

2) Построим образ треугольника DEF при симметрии относительно точки F.

Точка F является центром симметрии.

Тогда при центральной симметрии точка F отобразится сама на себя.

На продолжении отрезка DF отложим отрезок FD'  такой, что DF = FD'.  Тогда точка D' является образом точки D относительно центра симметрии - точки F.

На продолжении отрезка EF отложим отрезок FE'  такой, что EF = FE'.  Тогда точка E' является образом точки E относительно центра симметрии - точки F.

Соединим точки FD'E'.

Треугольник  D'E'F является образом треугольника DEF при центральной симметрии относительно точки F.

• Две точки симметричны относительно прямой (оси симметрии), если они лежат на одной прямой, перпендикулярной оси симметрии и на равном расстоянии от нее.

Рисунок 3.

2) Построим образ треугольника DEF при симметрии относительно прямой DF.

Так как точки D и F лежат на оси симметрии, то при отображении этих точек относительно прямой DF они перейдут сами в себя.

Проведем перпендикуляр к оси симметрии DF, отметим точку их пересечения - т.О.

На перпендикуляре от точки O отложим отрезок OE' такой, что
OE = OE'.

Соединим точки FDE'.

Треугольник  DE'F является образом треугольника DEF при симметрии относительно прямой DF.