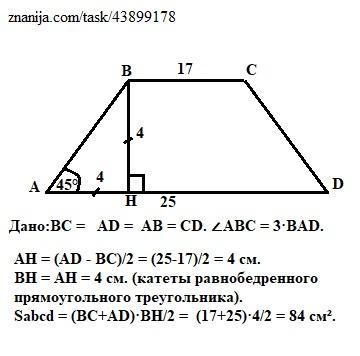
Один з кутів рівнобічної трапеції дорівнює втричі менший від іншого, а його основи дорівнють 17 см і 25 см. Обчисли площу трапеції.
Ответы
Ответ:
S = 84 см².
Пошаговое объяснение:
Углы при основаниях равнобедренной трапеции равны, а сумма углов, прилежащих к боковой стороне, равна 180°. Пусть острый угол трапеции (при большем основании) равен х, тогда тупой угол (при меньшем основании) равен 3х. Тогда 4х = 180° и х = 45°. В равнобедренной трапеции высота, проведенная из вершины тупого угла к большему основанию, делит его на отрезки, меньший из которых равен полуразности оснований.
В нашем случае этот отрезок равен (25-17):2 = 4см.
Тогда в равнобедренном (острый угол равен 45°} прямоугольном треугольнике, образованном найденным отрезком, высотой трапеции (катеты) и боковой стороной (гипотенуза) катеты равны. Значит высота трапеции равна 4см.
Площадь трапеции равна произведению полусумме оснований на высоту.
S = (17+25)•4/2 = 84 см².