Предмет: Алгебра,
автор: GlinkaMatemaster666
Решите 2 неравенства:
Приложения:
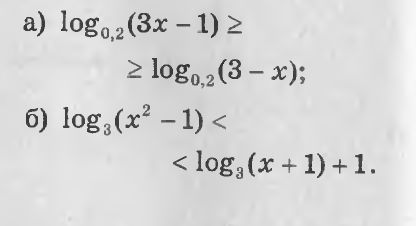
Ответы
Автор ответа:
0
a)
log[0,2] (3x-1) >= log [0,2] ( 3-x)
0< (3x-1) <= ( 3-x)
1/3 < x <= 1 - это ответ
б)
log[3] (x^2-1) < log [3] ( x+1) +1
log[3] (x^2-1) < log [3] ( x+1) + log [3] (3)
0 < (x^2-1) < 3( x+1)
|x| > 1 и (x^2-1) < 3( x+1)
|x| > 1 и (x^2-3x-4) < 0
|x| > 1 и -1 < x < 4
1 < x < 4 - это ответ
log[0,2] (3x-1) >= log [0,2] ( 3-x)
0< (3x-1) <= ( 3-x)
1/3 < x <= 1 - это ответ
б)
log[3] (x^2-1) < log [3] ( x+1) +1
log[3] (x^2-1) < log [3] ( x+1) + log [3] (3)
0 < (x^2-1) < 3( x+1)
|x| > 1 и (x^2-1) < 3( x+1)
|x| > 1 и (x^2-3x-4) < 0
|x| > 1 и -1 < x < 4
1 < x < 4 - это ответ
Похожие вопросы
Предмет: Английский язык,
автор: alina0366
Предмет: Математика,
автор: somilossoly
Предмет: Английский язык,
автор: burunduck77
Предмет: Физика,
автор: milan96