Предмет: Алгебра,
автор: Taesarah03
2,3,4 номера пожалуйста ......
Приложения:
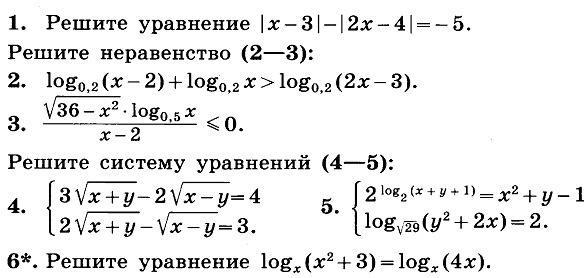
Taesarah03:
5 тоже пожалуйста если не сложно у меня не правильно выходит
Ответы
Автор ответа:
3
Ответ:
добавила текст , обнови страничку
Похожие вопросы
Предмет: Английский язык,
автор: MrTrololo111
Предмет: Русский язык,
автор: Predatormk3
Предмет: Английский язык,
автор: lizicucqiridze
Предмет: Английский язык,
автор: знаникп
Предмет: Химия,
автор: SeregaBEN123