Предмет: Алгебра,
автор: kurochka1234
ПОМОГИТЕ
СРОЧНО
30 БАЛЛОВ
ВО ВЛОЖЕНИИ
Приложения:
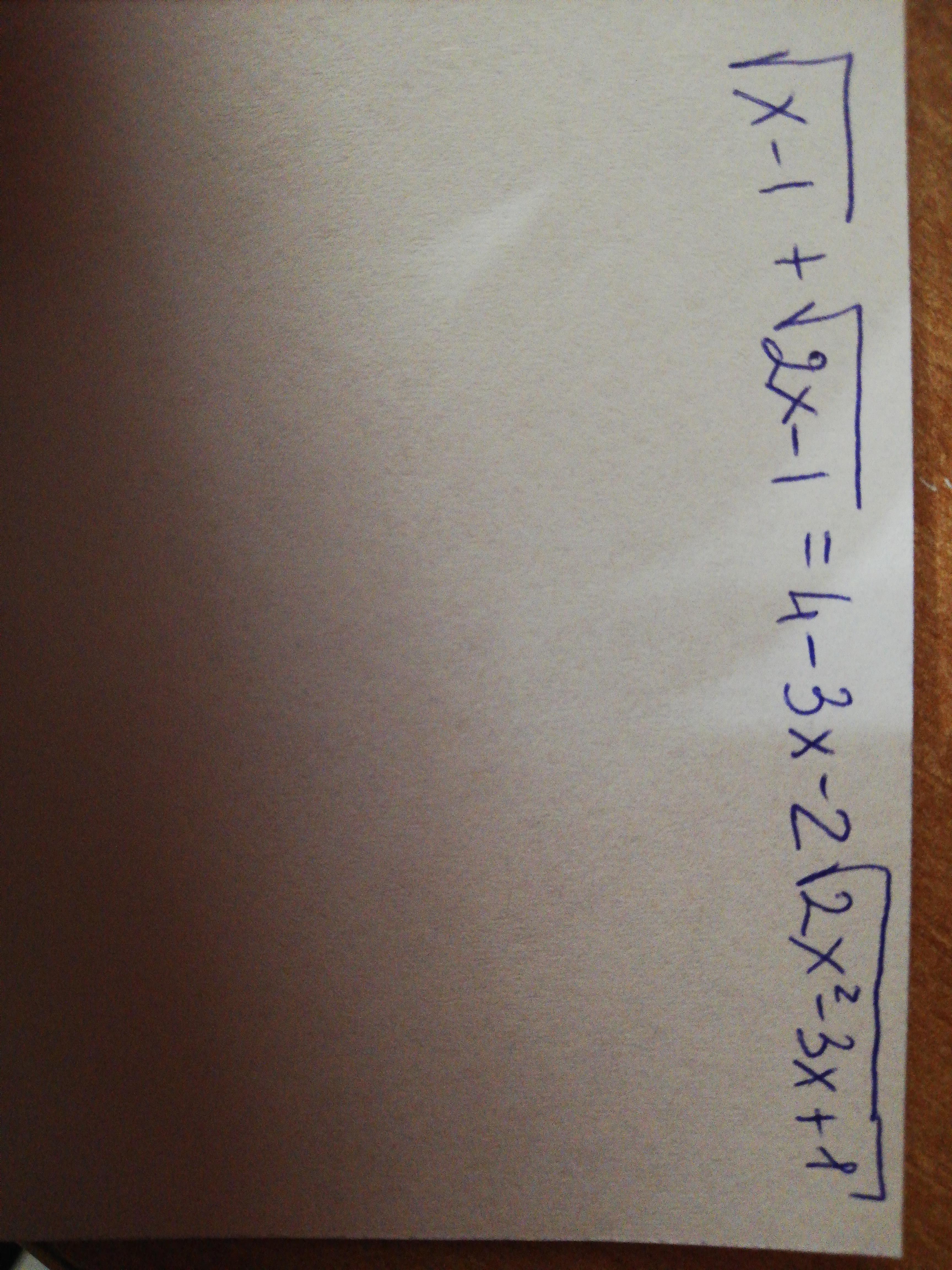
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Egor1082423
Предмет: Русский язык,
автор: kris123451
Предмет: Русский язык,
автор: в127тпс
Предмет: Русский язык,
автор: MrKonor611