Question

Срочно !!!!
Помогите пожалуйста .
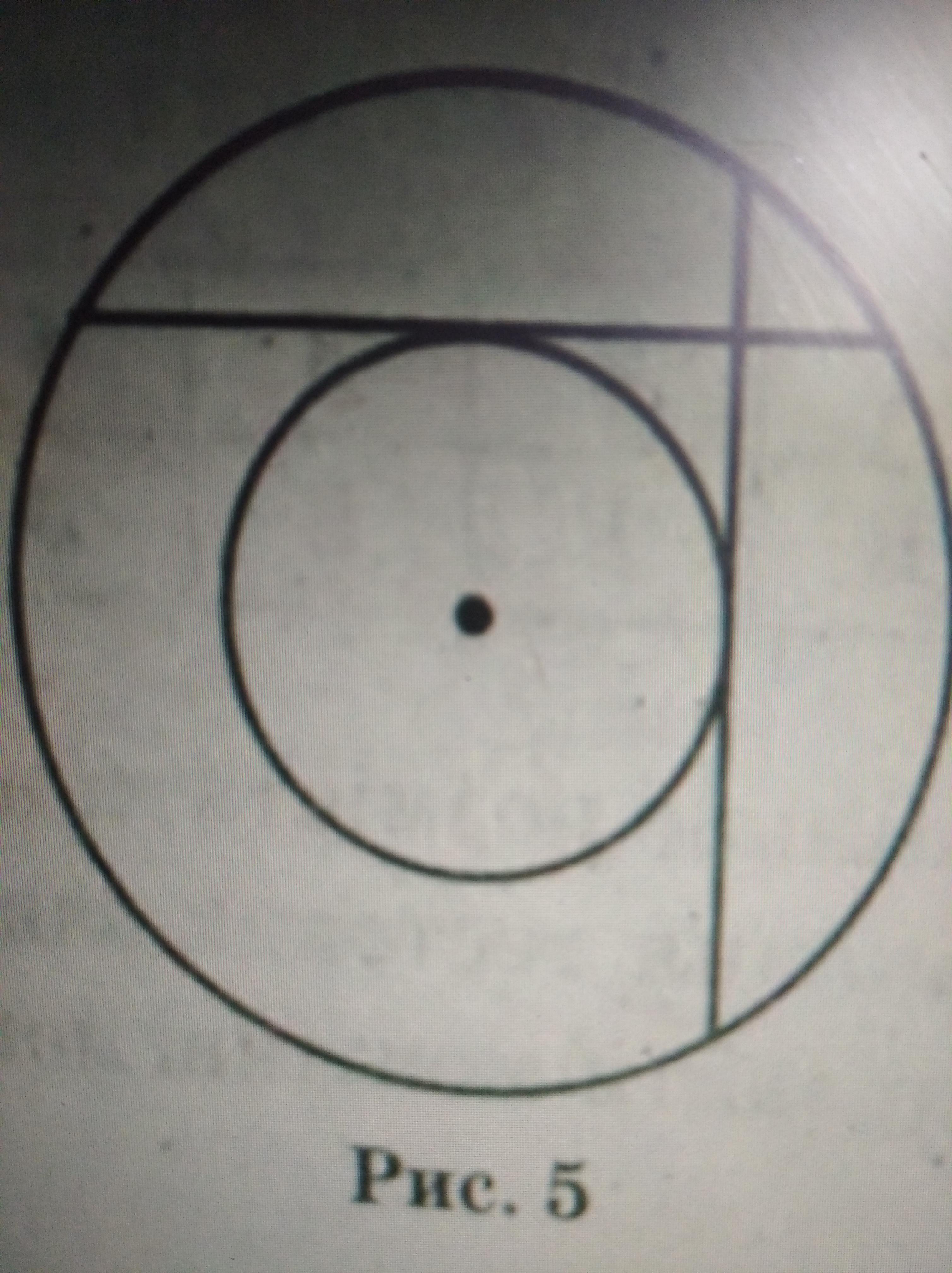
Дві рівні та взаємно перпендикулярні хорди кола точкою перетину діляться на частини завдовжки 4см і 16 см . Знайдіть рідіус кола , яке дотикається до цих хорд і має спільний центр із поданим колом .

Answer 1

Ответ:

6 см

Объяснение:

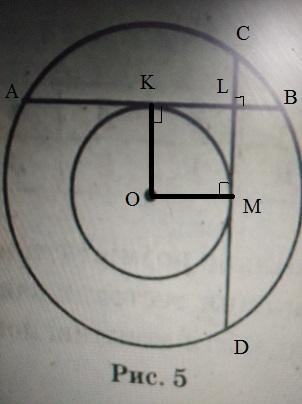
Радиусы OK и ОМ, проведённые в точки касания хорд с малой окружностью, будут перпендикулярны касательным - хордам АВ и CD. Но также, по свойству диаметра, перпендикулярного хорде, точки К и М будут лежать на серединах отрезков АВ и CD.

АВ=CD=AL+LB=16+4=20см

AK=KB=20/2=10см

KL=KB-LB=10-4=6см

KLMO - квадрат, поскольку все его смежные стороны имеют между собой прямой угол (2 - как радиусы к касательным, 1 - по условию перпендикулярности хорд, и оставшийся тоже получается 90°), и две его смежные стороны ОК и ОМ равны радиусу.

Значит ОМ=KL=6см