Предмет: Математика,
автор: helpmeplease44343
Найти определённый интеграл методом замены переменной
Приложения:
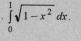
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: nadj5555
Предмет: Английский язык,
автор: elokhin11
Предмет: Английский язык,
автор: Vias
Предмет: Математика,
автор: Ко456788онхээ