Предмет: Математика,
автор: Snuppiman
Исследовать сходимость числового ряда! Очень нужно!
Приложения:
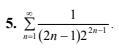
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
здесь тоже пользуясь свойствами прелелов исходное выражение можно упростить
тогда
и теперь признак Даламбера
q < 1, то ряд сходится
Похожие вопросы
Предмет: Русский язык,
автор: yulyaartemowa2005
Предмет: Английский язык,
автор: Stason2006
Предмет: Окружающий мир,
автор: ninamikushkina
Предмет: Биология,
автор: GaisinaArina
Предмет: Алгебра,
автор: Hyperquick111