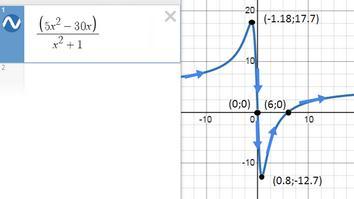
Дослідити функцію
Допоможіть, будь ласка
Даю 100 балів
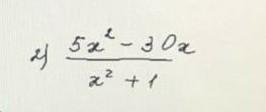
Ответы
Ответ:
Пошаговое объяснение:
1) ООФ
здесь знаменатель всегда ≠ 0, поэтому ООФ - вся числовая ось
2) функция не тригонометрическая
3) пересечение с осью оу (х = 0)
у(0) = 0 точка (0;0)
с осью ох (у=0)
из дроби приравниваем к 0 числитель
5х² -30х = 5х(х -6) ⇒
х₁ = 0 точка (0;0)
х₂ = 6 точка (6;0)
4) критические точки
для нахождения производной используем
тогда
y'(x) = 0
10(3x² +x-3) = 0 ⇒ (значения определяем с точностью до 0,01)
y(x₁) ≈ 17.707 точка (-1,18; 17,7)
у(х₂) ≈ -12,7 точка (0,8; -12,7)
5) промежутки возрастания и убывания. экстремумы
локальные экстремумы
у(≈-1,18) ≈ 17,7 - локальный максимум
у(≈0,8) ≈ -12,7 - локальный минимум
промежутки монотонности
(-∞ ;-1.18) f'(x) > 0 функция возрастает
(-1.18; 0.8) f'(x) < 0 функция убывает
(0.8; +∞) f'(x) > 0 функция возрастает
6)
6) поскольку промежуток ООФ, то концы промежутка (-∞; +∞)
при х → -∞ f(x) f(x) → -∞
при х → +∞ f(x) f(x) → +∞
7)
точки (0;0) (6;0)
(-1,18; 17,7) - локальный максимум
(0,8; -12,7) - локальный минимум
промежутки монотонности
(-∞ ;-1.18) f'(x) > 0 функция возрастает
(-1.18; 0.8) f'(x) < 0 функция убывает
(0.8; +∞) f'(x) > 0 функция возрастает
график прилагается