Предмет: Алгебра,
автор: Ksenia20042021
Найти площадь фигуры, ограниченной осями координат, графиком функции y=x^2+3 и прямой x=2
Ответы
Автор ответа:
0
Объяснение:
Ответ: S=8,66667 кв. ед.
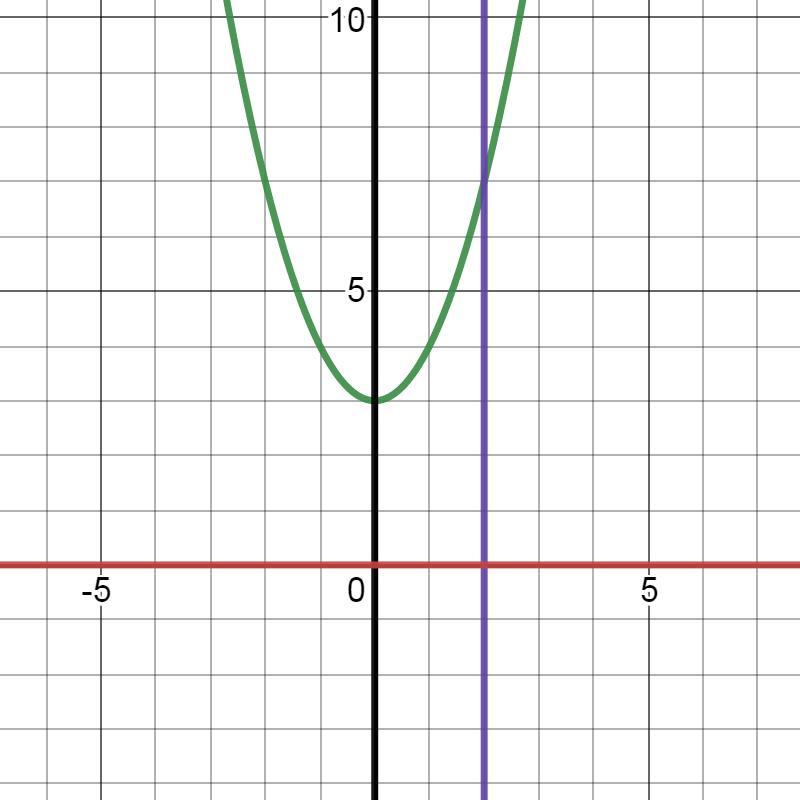
у=х²+3 - зелёный цвет.
у=0 - красный цвет.
х=0 - чёрный цвет.
х=2 - фиолетовый цвет.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Zaremaegi
Предмет: Русский язык,
автор: garmakhanda
Предмет: Окружающий мир,
автор: sdanyn120
Предмет: Русский язык,
автор: maksimnaboka123