Предмет: Алгебра,
автор: minateddy
Пожалуйста помогите с Алгеброй.
Дам 25 баллов.
Приложения:
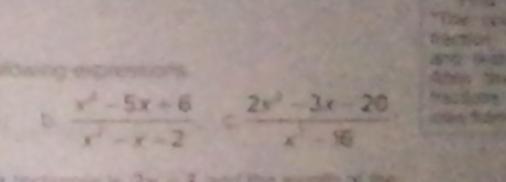
minateddy:
Щас попробую.
плохо видно условие
Ответы
Автор ответа:
1
Ответ: нет решений .
в первом в числителе x^2-5x+6
а мне кажется, что минус
Спасибо вы мне очень помоглиҚ
Похожие вопросы
Предмет: Русский язык,
автор: hasanalakbarzadze
Предмет: Английский язык,
автор: dragmedown1806
Предмет: Русский язык,
автор: elenabobrova
Предмет: История,
автор: Soundmoon
Предмет: Другие предметы,
автор: vladimirlut