Предмет: Геометрия,
автор: ameba1obuknovennai
вычислите площадь фигур, ограниченной линиями:
( с рисунком пожалуйста)
Приложения:
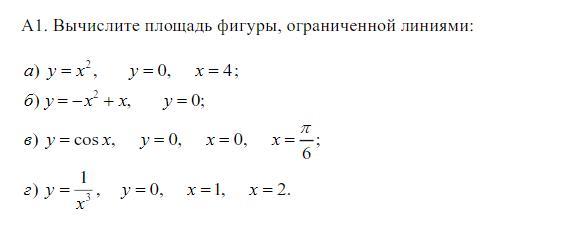
Ответы
Автор ответа:
1
Ответ:
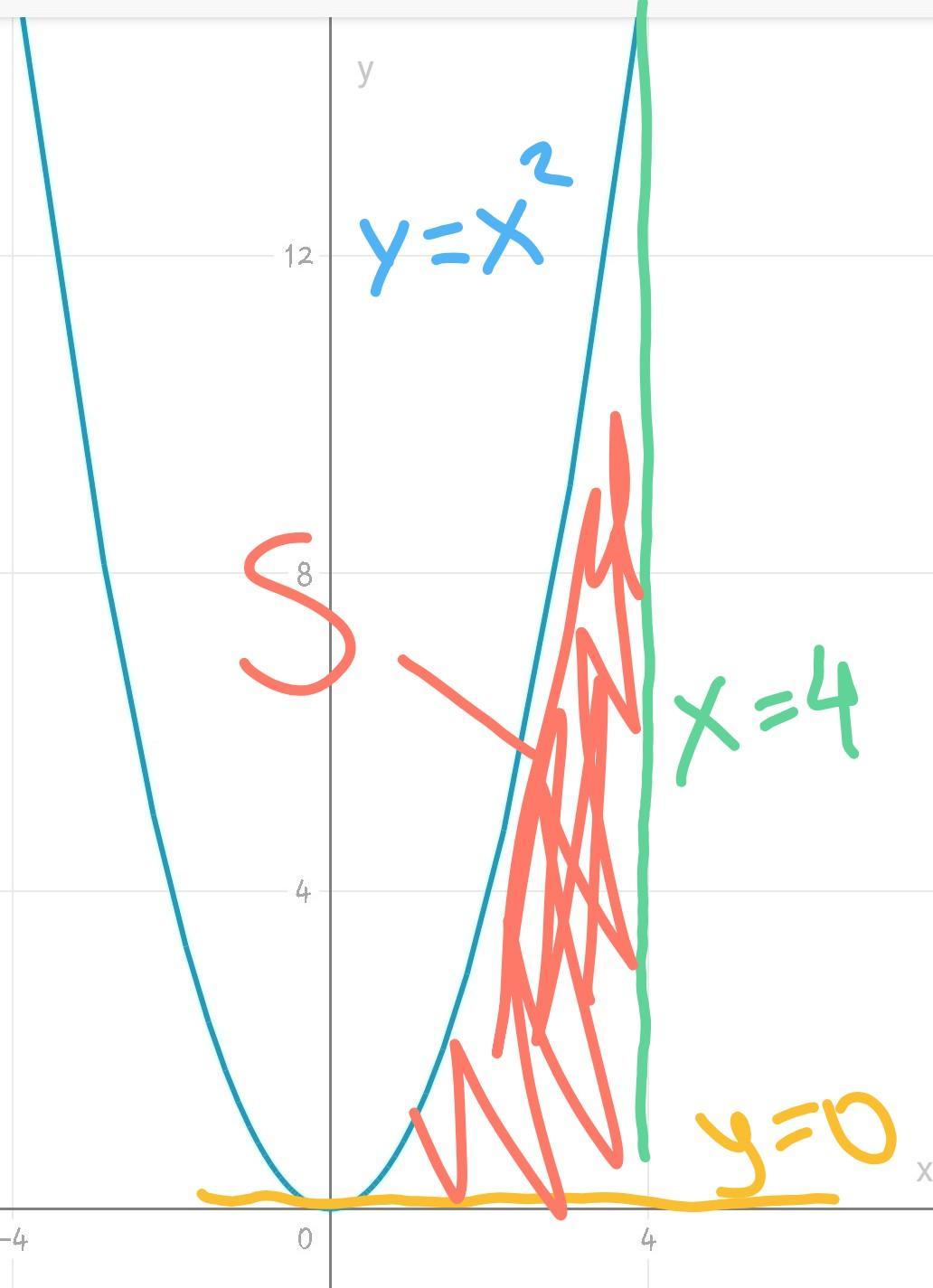
a) рисунок1
Пределы: 0 и 4
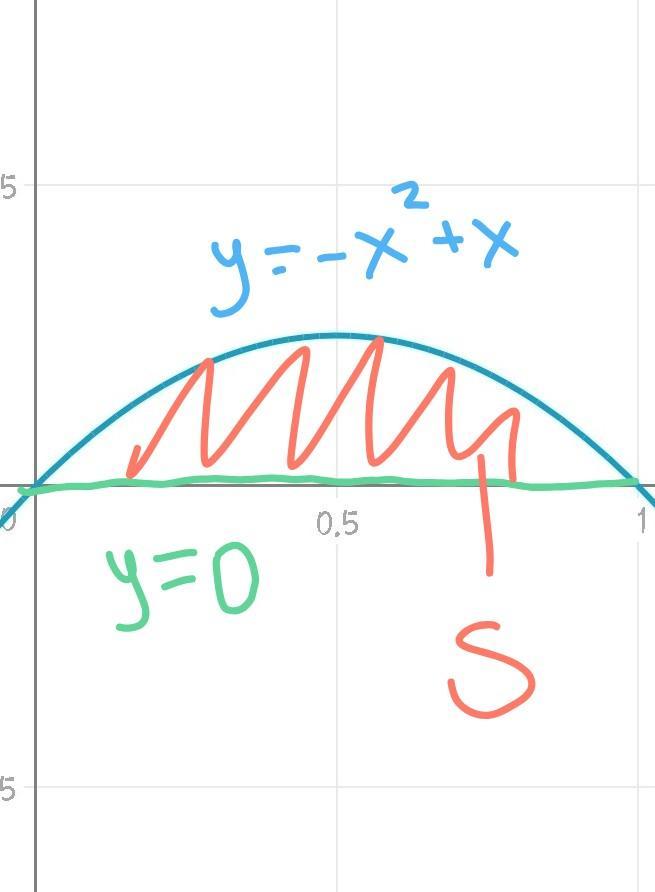
б) рисунок2
Пределы: 0 и 1
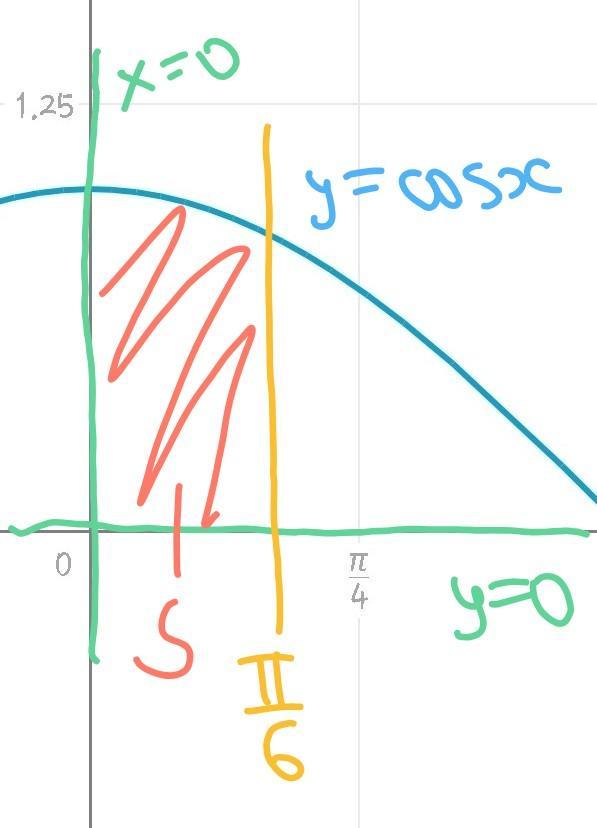
в) рисунок 3
Пределы: 0 и П/6
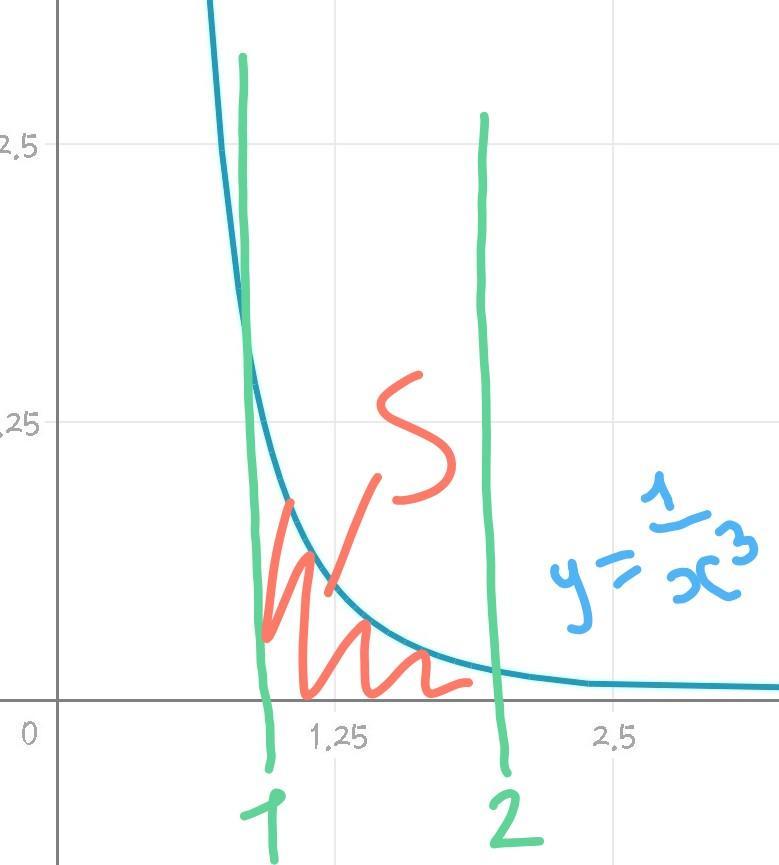
г) рисунок 4
Пределы: 1 и 2
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: boomrow
Предмет: Українська мова,
автор: tolstov56894
Предмет: Русский язык,
автор: gazina67
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: strobykin02