Предмет: Геометрия,
автор: golywolf4
Помогите с геометрией пожалуйста, срочнаа
Приложения:
Ответы
Автор ответа:
1
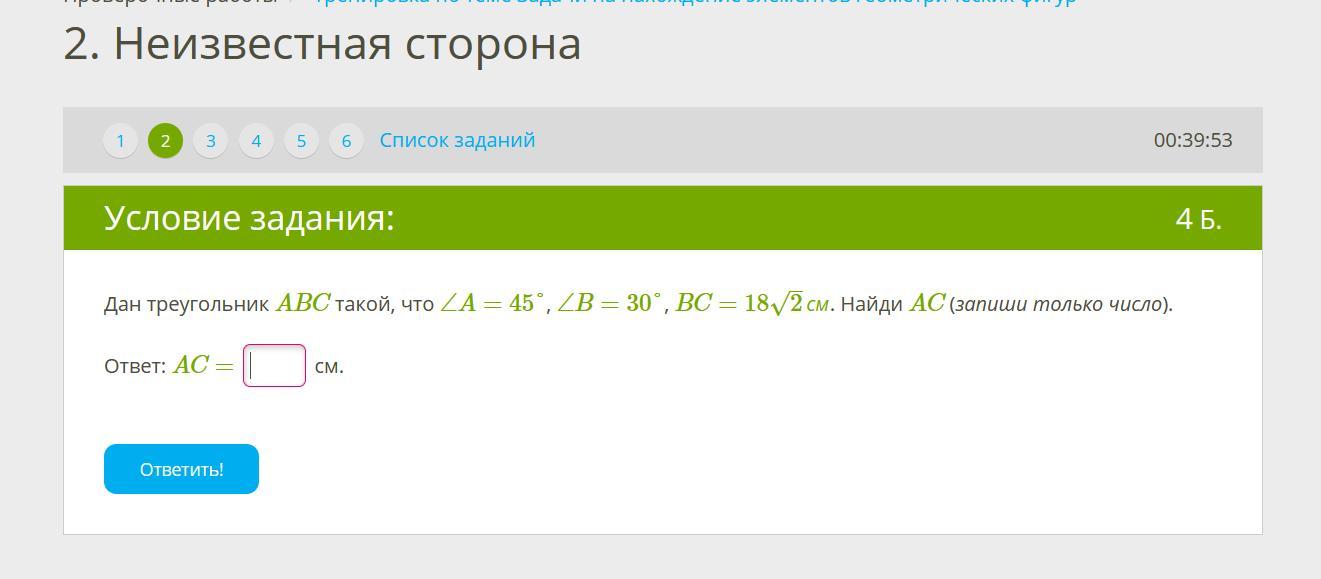
<C = 180-(<A + <B) = 180-(30+45) = 75°.
Теперь нам известна сторона BC, и прилежащие к нему углы.
Остальные стороны можем найти по теореме Синусов:
Вывод: AC = 18.
Автор ответа:
1
Решение:
применяя теорему синусов:
Ответ: АС = 18см
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: irinda232
Предмет: Русский язык,
автор: Toriva
Предмет: Математика,
автор: пирожок29