Предмет: Математика,
автор: 3102422
замена: (x+1/x)=t Помогите решить
Приложения:
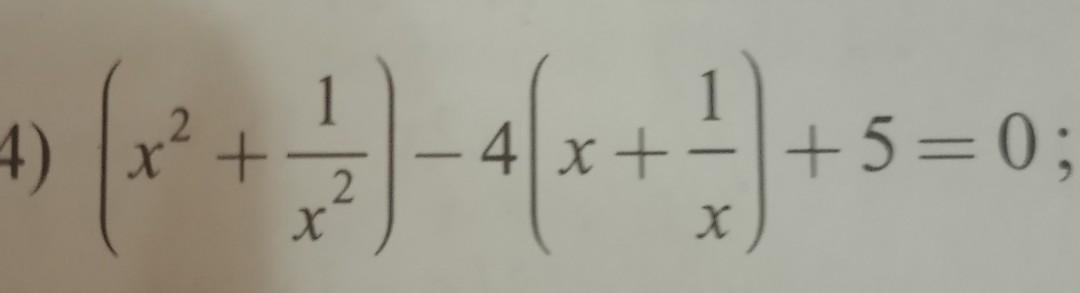
Ответы
Автор ответа:
1
Ответ:
Если t₁ = 3 , то:
Если t₂ = 1 , то:
∅
Таким образом:
Пошаговое объяснение:
3102422:
(x^2+1/x^2) это же не t^2
это т^2)
1^2 = 1
поэтому я и возвел т в квадрат)
поэтому я и возвел т в квадрат)
нет, это не t^2... по формуле (а это формула "квадрат суммы") есть еще и удвоенное произведение... потому, t^2=x^2+(1/x^2)+2... и решение будет...
ааааааа точно,был бы квадрат за скобкой)
все дошло,спасибо)
хотя нет не понял,откуда 2?
Все решил,спасибо за подсказку)
прости что сразу не решил верно.
прости что сразу не решил верно.
Похожие вопросы
Предмет: Русский язык,
автор: zhannatmusina
Предмет: Русский язык,
автор: asminkina51
Предмет: Русский язык,
автор: asminkina51
Предмет: История,
автор: 12MeLoMaNkA12
Предмет: Русский язык,
автор: Умняха2007