Предмет: Математика,
автор: pavlovdenis2004
Помогите прошу решить задачи
Приложения:
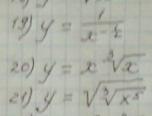
Ответы
Автор ответа:
0
Відповідь:
Покрокове пояснення:
Похожие вопросы
Предмет: Немецкий язык,
автор: Egorev10
Предмет: Английский язык,
автор: jashckovanton
Предмет: Қазақ тiлi,
автор: сергей214
Предмет: Другие предметы,
автор: ник5325
Предмет: Геометрия,
автор: hikagirl1