Question

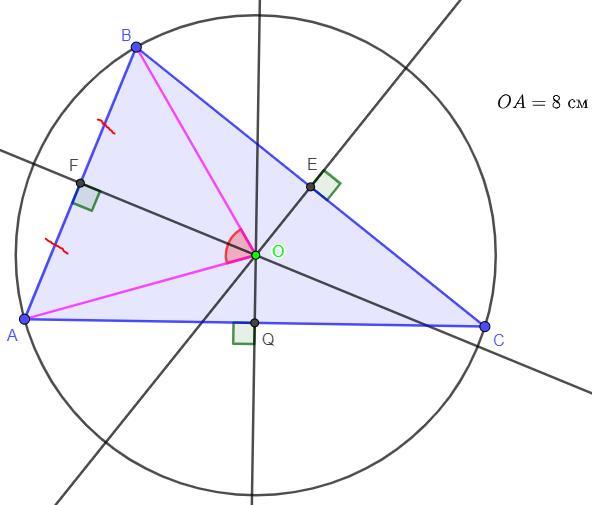
Серединні перпендикуляри до сторін трикутника АВС перетинаються в точці О.Знайдіть довжину сторони АВ,якщо ОА=8см, АОВ=60°​

Answer 1

Ответ:

AB = 8 см

Объяснение:

Дано: ОА = 8см, ∠АОВ = 60°; OQ,OE,OF - cерединні перпендикуляри

Знайти: AB - ?

Розв'язання:

За теоремою точка перетину серединних перпендикулярів є центром описаного кола, отже за умовою точка O - центр вписаного кола трикутника ΔABC, тоді OA = OB як радіуси описаного кола і звідци трикутник ΔAOB - рівнобедрений за означенням.

Розглянемо рівнобедрений трикуник ΔAOB. Так як за умовою OF - серединний перпендикуляр, то відрізок OF - медіана трикутника ΔAOB.

За теоремою медіана рівнобедреного трикутника є його бісектрисою і висотою, отже OF - бісектриса кута ∠AOB. За означенням бісектриса ∠AOF = ∠BOF = ∠AOB : 2 = 60° : 2 = 30°.

Розглянемо прямокутний трикуник ΔAOF (OF ⊥ AB за умовою).

$\sin \angle AOF = \dfrac{AF}{AO} \Longrightarrow AF = AO \cdot \sin \angle AOF = 8 \cdot \sin 30^{\circ} = 8 \cdot 0,5 = 4$ см.

Так як OF - медіана трикутника ΔAOB, то AF = BF, тоді за основною властивістю відрізка:

AB = AF + FB = 2BF = 2AF = 2 * 4 = 8 см.