Предмет: Геометрия,
автор: vecikjan
Помогите пожалуйста, срочно!
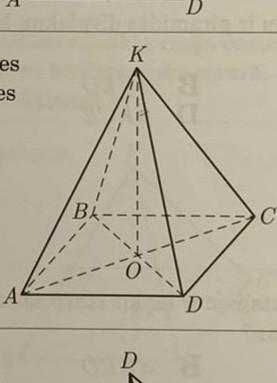
Сторона правильной четырехугольной пирамиды имеет длину 6√2, а противоположные боковые грани перпендикулярны. Диагональное сечение пирамиды равно?
Приложения:
vecikjan:
Я жду ваши ответы
Ответы
Автор ответа:
1
Ответ: Из точки К на основания двух противоположных боковых граней опустим апофемы КН и КН1. Угол НКН1 = 90 градусов (так как грани перпендикулярны и КН ⊥ AD, КН1 ⊥ BC). Из условия задачи следует, что НН1 = 6√2. Рассмотрим ΔНКН1 - прямоугольный. В нем КН=КН1=НН1/√2=6√2/√2=6. Теперь рассмотрим ΔОКН - тоже прямоугольный, тк КО - высота пирамиды. ОН=1/2 * НН1= 6√2/2=3√2.
По теореме Пифагора: КО² = КН² - ОН² = 6²-18 = 18 ⇒ КО = 3√2.
АС - диагональ квадрата ABCD, она равна DC*√2 = 6√2*√2 = 12.
Площадь ΔКАС(площадь диагонального сечения) = 1/2 * КО * АС =
= 1/2 * 3√2 * 12 = 18√2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: АМИРГАЛИНА
Предмет: Русский язык,
автор: sorvin96
Предмет: Русский язык,
автор: 2браер25
Предмет: Русский язык,
автор: Владислав2007
Предмет: Математика,
автор: uplay9663good