Предмет: Математика,
автор: x5ihx
Срочно!!! даю 35 балов!!!! 2 вложения
Знайти похідну функцій:
Приложения:
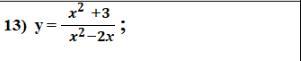
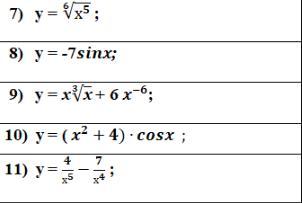
Ответы
Автор ответа:
2
7
8
9
10
11
13
xjxjxjjcnc:
Добрый вечер, Мирослава не могли бы Вы помочь? Если можете помогите пожалуйста . По геометрии
Прошу очень нужно
Похожие вопросы
Предмет: Русский язык,
автор: anisimovt45
Предмет: Қазақ тiлi,
автор: ntabylby
Предмет: Русский язык,
автор: Кашка74
Предмет: Другие предметы,
автор: HELPERSKINE
Предмет: Другие предметы,
автор: арина123456789o