Question

Здравствуйте!

Вот эта задача ввела в ступор, никак не понимаю как её сделать. Буду благодарен за помощь!

Answer 1

Ответ:

Объяснение:

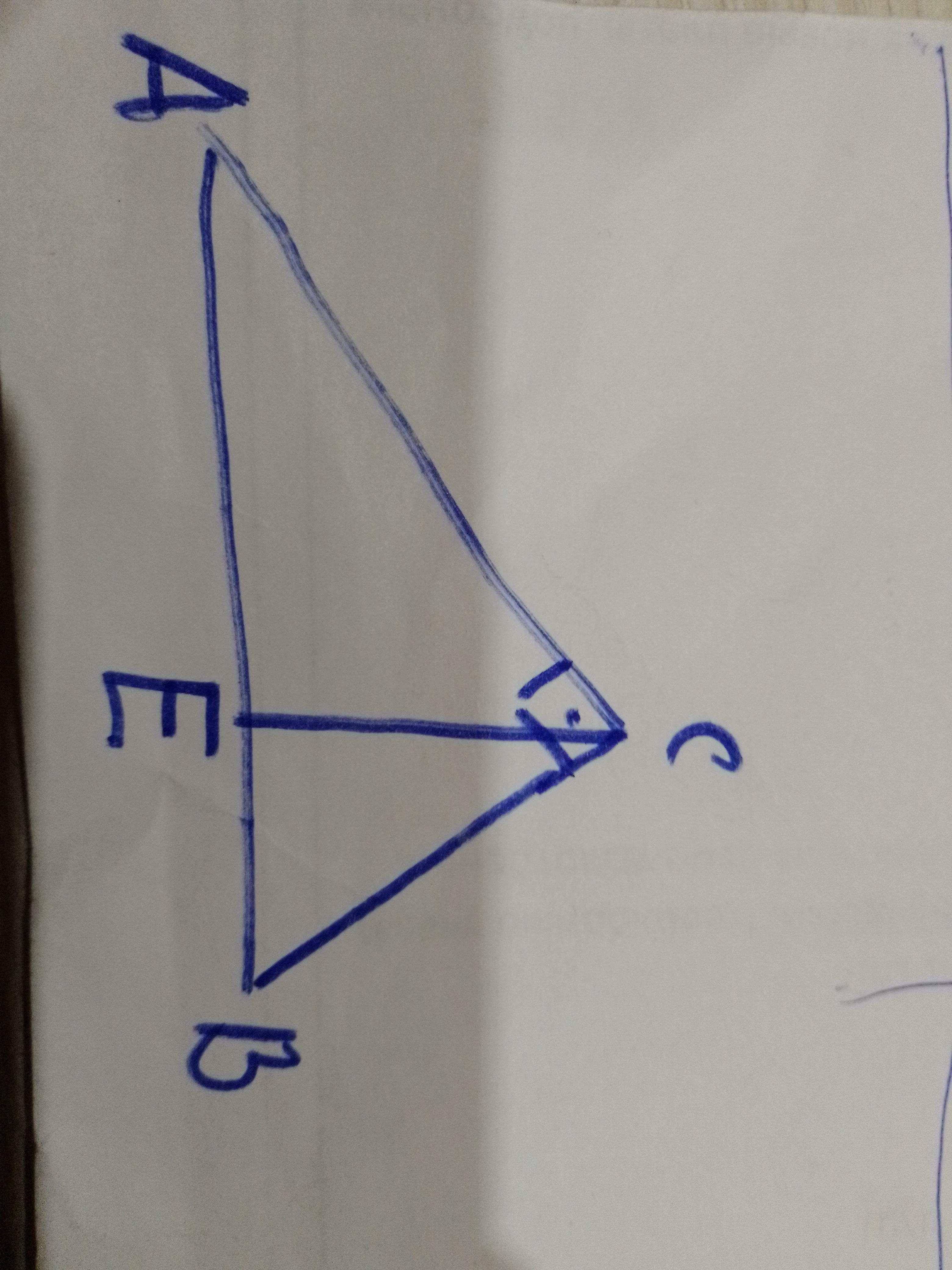
Дано ∆АВС, <С=90

<(СЕ)(АВ)=90

Р(АЕС)=12,. Р(ВЕС)=5

Р(АВС)

Решение.

Р(АВС)=АВ+АС+ВС

Р(АЕС)=АС+АЕ+СЕ)=12

Р(ВЕС)=ВС+ВЕ+СЕ)=5

Для решения системы уравнений вычтим и сложим обе части между собой

Р(АВС)=АВ+АС+ВС;. АВ=АЕ+ЕВ,

12+5=АС+АЕ+СЕ+ВС+ВЕ+СЕ

17= Р(АВС)+2СЕ

12-5=АС+АЕ+СЕ- ВС -ВЕ -СЕ

7 = АС+АЕ -ВС -ВЕ

Воспользуемся свойством высоты прямоугольного треугольника h^2=AE*EB,

AC^2=AE^2+CE^2

BC^2=BE^2+CE^2. вычтим из

АС^2 -BC^2=AE^2 -BE^2

AC^2 + BC^2 = AE^2+2CE^2+BE^2

AB^2=(AE+BE)^2=AE^2+2AE*BE+BE^2

вычтим/сложим одно из/с другого,

2СЕ^2 - 2АЕ*ВЕ;

. СЕ^2=АЕ*ВЕ. CE=AC*BC/AB

2АВ^2=2AE

P(ABC)=17 - 2√(AE*BE)