Предмет: Геометрия,
автор: supersonichedgehog
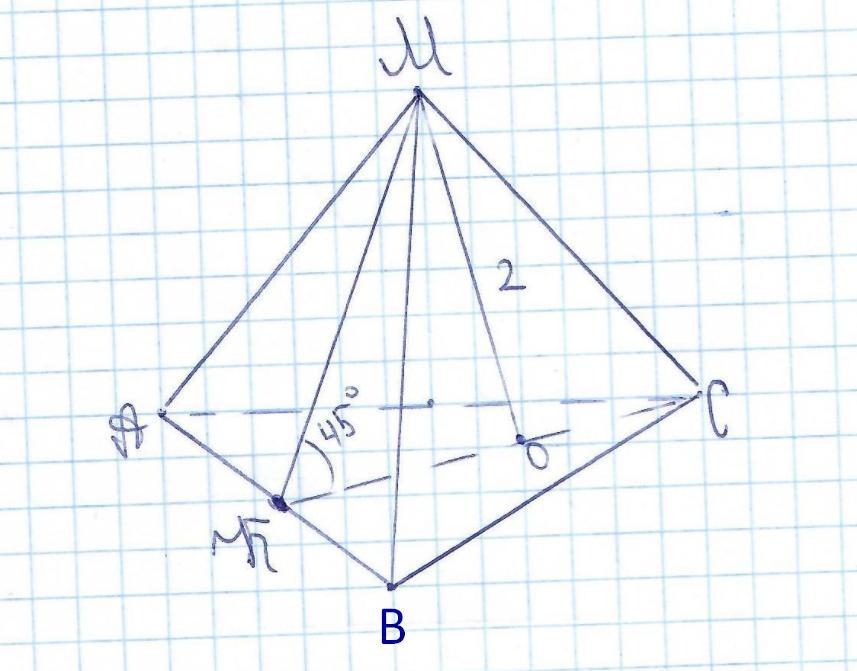
Высота правильной треугольной пирамиды равна 2, а двугранный угол при основании 45°. Найдите площадь боковой поверхности пирамиды S. В ответ запишите S/корень из 6. С решением, будьте любезны
Ответы
Автор ответа:
6
===========================РЕШЕНИЕ=============================
1) Рассмотрим ΔКОМ: ∠О=90°, ∠К=45° ⇒ ∠М=180°-90°-45°=45°, значит треугольник равнобедренный, тогда МО=ОК=2
по т.Пифагора найдём КМ:
КМ=2√2=h - апофема
2) - медиана
, так как медианы в точке пересечения делятся в отношении 1:2, значит КО=1 часть, КС=3 части
Подставим значения:
(*6)
- сторона основания ΔАВС
3) Sбок=
Sбок=
Sбок=
Sбок=
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: etaranenko
Предмет: Українська мова,
автор: mishadtm
Предмет: Русский язык,
автор: kirpo02
Предмет: Русский язык,
автор: mashnovaleksandr