Предмет: Алгебра,
автор: ilya282o
помогите ПОЖАЛУЙСТА СРОЧНО
Приложения:
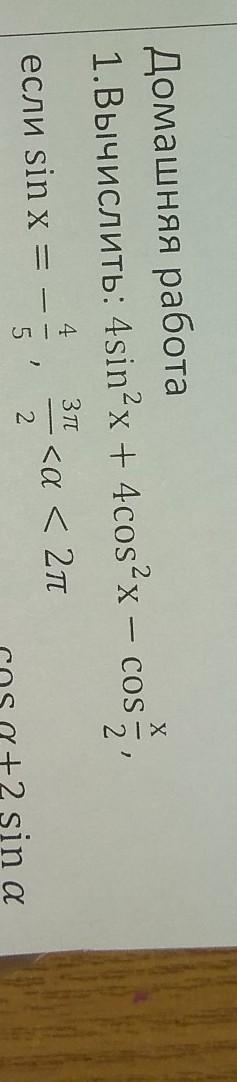
Ответы
Автор ответа:
2
Ответ:
1.
Угол х принадлежит 4 четверти, значит угол х/2 - 3 четверти, cosx/2 < 0
ffufbrnjfjt:
Здравствуйте, помогите пожалуйста мне очень нужна ваша помощь
Похожие вопросы
Предмет: Английский язык,
автор: alinaashigova
Предмет: Английский язык,
автор: ученик484
Предмет: Русский язык,
автор: Гульмира23
Предмет: Математика,
автор: Vfdhbfeeyjvddgn
Предмет: Математика,
автор: Аноним