Предмет: Алгебра,
автор: cbjgy35072
разрешите уравнение 8клас
Приложения:
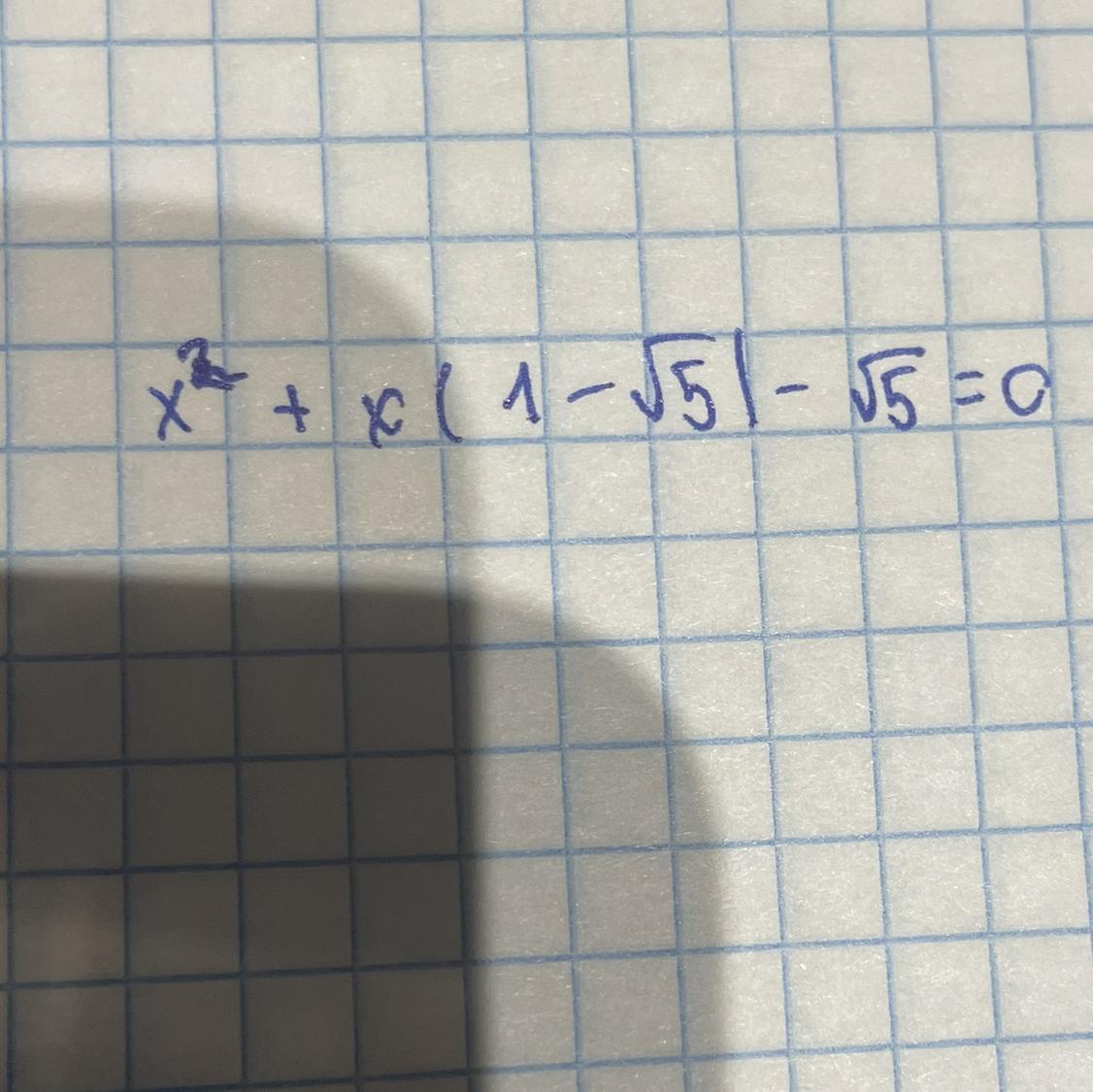
Ответы
Автор ответа:
0
Ответ:
-1; √5
Объяснение:
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: qwert22asd
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: wow12wow
Предмет: Алгебра,
автор: Алькатрон
Предмет: Физика,
автор: dahakrav1234