Предмет: Алгебра,
автор: coollione
Почему нельзя разделить на cosx, чтобы получилось уравнение с tgx?
Приложения:
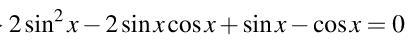
colncez:
вопрос был почему нельзя разделить на cosx, а не решить уравнение
Ответы
Автор ответа:
0
Автор ответа:
0
Поделить-то можно, поскольку точки, в которых не являются корнями (при любом из двух значений синуса) данного уравнения, т.е. потери корней не произойдёт.
Но такой ход не оставит уравнения на , поскольку есть синус во второй степени. Даже если поделить на косинус в квадрате -- есть синус в первой степени, который оставит лишний косинус.
мой подобный ответ удалили как не полный)))
Похожие вопросы
Предмет: Українська мова,
автор: вправа215
Предмет: Українська мова,
автор: Аноним
Предмет: Русский язык,
автор: KULAMIN05
Предмет: Математика,
автор: leazy
Предмет: Математика,
автор: zolotaat