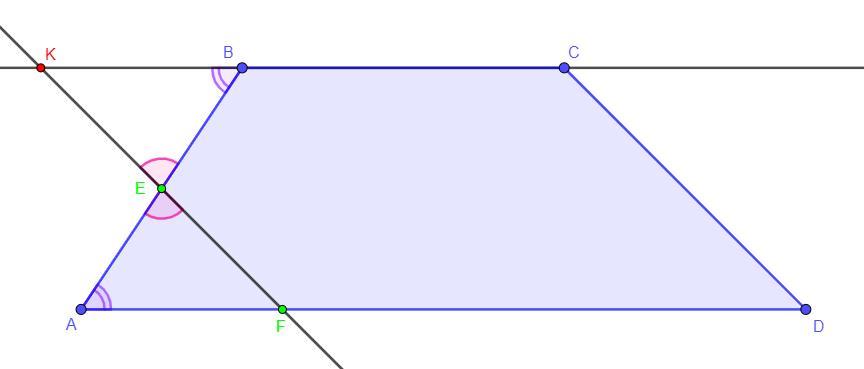
через точку Е - середину боковой стороны AB трапеции ABCD -проведена прямая, параллельная стороне CD и пересекающая основание AD в точке F. Найдите сторону CD, если EF = 10 см.
Ответы
Ответ:
CD = 20 см
Объяснение:
Дано: ABCD - трапеция, AE = BE, EF║CD, EF = 10 см
Найти: CD - ?
Решение:
Проведем прямую BC. Пусть BC ∩ EF = K.
Треугольник ΔAEF = ΔBEK по второму признаку равенства треугольников, так как по условию AE = BE и угол ∠AEF = ∠BEK как вертикальные углы, а угол ∠KBA = ∠DAB по теореме как внутренние накрест лежащие углы при параллельных прямых, так как по определению трапеции BC║AD (по условию ABCD - трапеция; AB - секущая).
Так как треугольник ΔAEF = ΔBEK, то соответствующие элементы треугольников равны, тогда EF = KE = 10 см.
По основному свойству отрезка:
KF = KE + FE = 10 + 10 = 20 см.
По определению KFDC - параллелограмм, так как по условию EF║CD и BC║AD, так как по условию ABCD - трапеция.
По свойствам параллелограмма (KFDC) его противоположные стороны равны, тогда KF = CD = 20 см.