Предмет: Математика,
автор: Alex62345
Решить неопределённые интегралы методом подстановки.
Приложения:
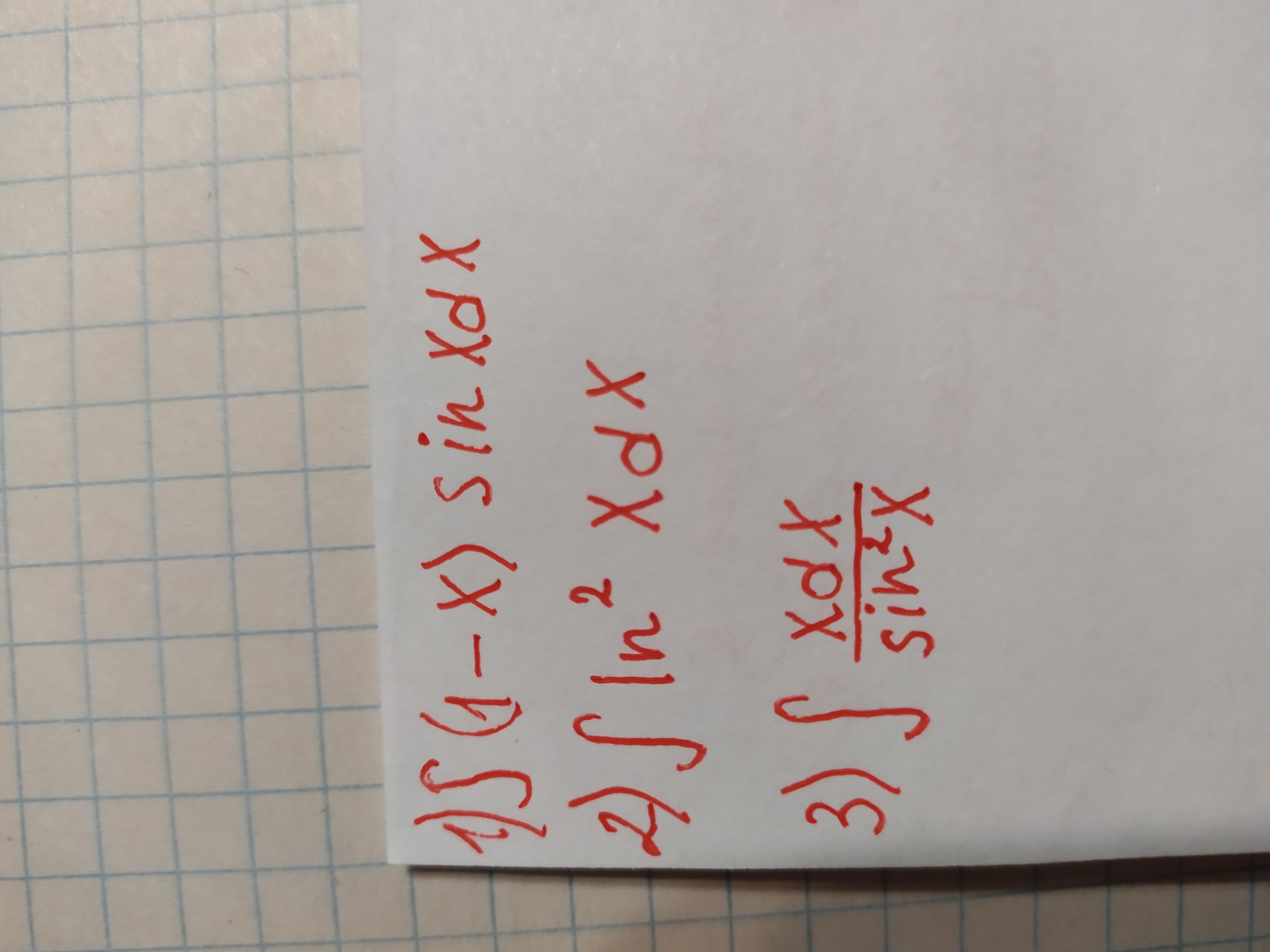
Miroslava227:
они все решаются по частям, а не подстановкой
решать?
Да
Ответы
Автор ответа:
1
Все интегралы решаются по частям.
1.
2.
3.
Здравствуйте, извините что беспокою вас в столь поздний час. Мне нужна ваша помощь с физикой. Буду очень благодарна, если вы посмотрите моё задание)
Похожие вопросы
Предмет: Русский язык,
автор: tanisadal
Предмет: Русский язык,
автор: lalal12332jjj132
Предмет: Қазақ тiлi,
автор: Sanzharaliaska
Предмет: Другие предметы,
автор: яяфйфы
Предмет: Математика,
автор: Vdjodhdbd