40 БАЛЛОВ
только ответы, пожалуйста
Ответы
Ответ:
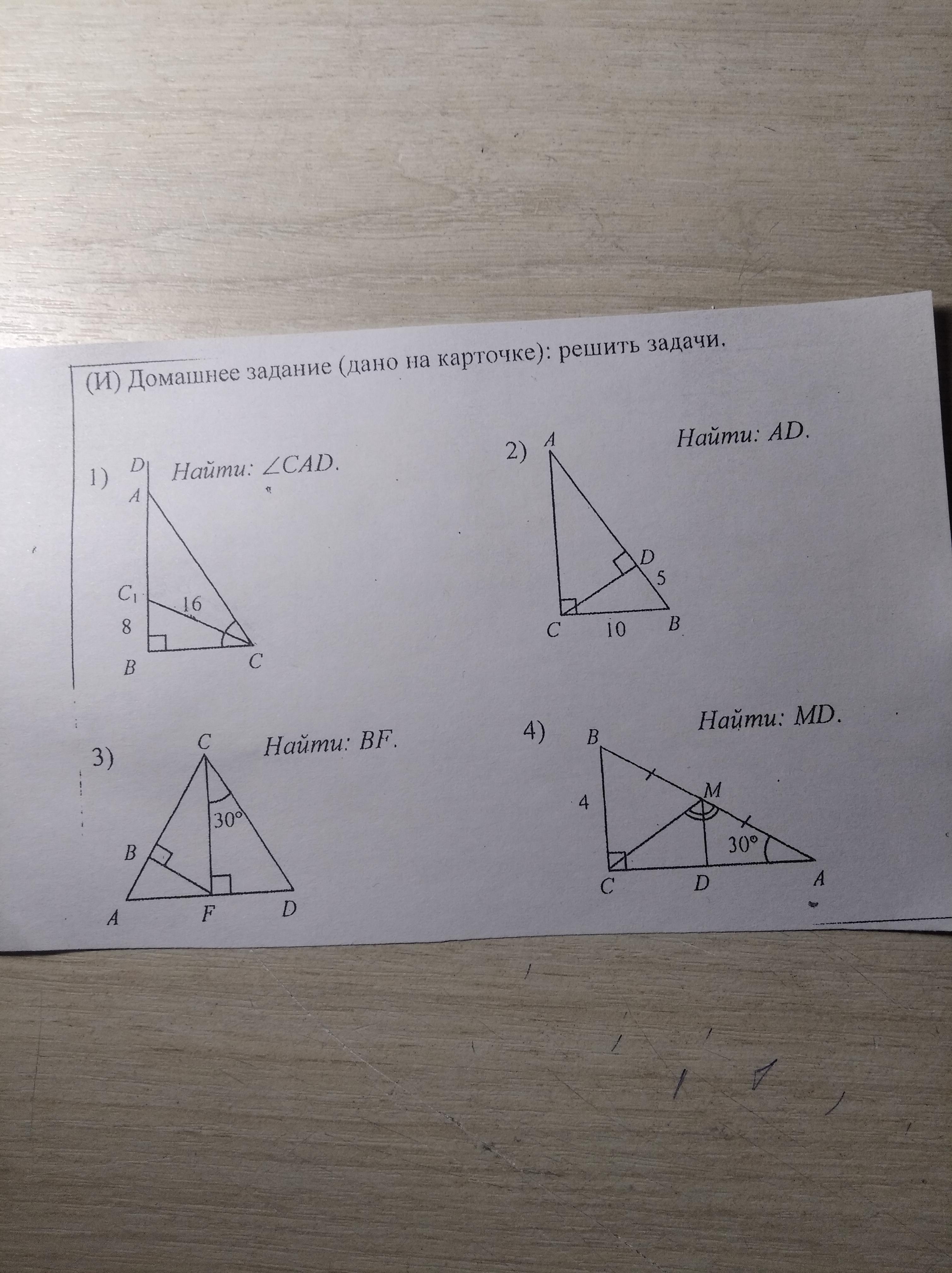
1-Дано: ΔАВС — прямоугольный (∠В=90°), ЕС = 16, ЕВ = 8, ∠ЕСВ = ∠ЕСА.
Найти: ∠САD.
Решение:
В ΔЕВС катет ЕВ = 1/2 гипотенузы ЕС ⇒ ∠ЕСВ = 30° (по свойству прямоуг. треугольника).
∠ЕСВ = ∠ЕСА (по условию) = 30°. ∠С = 30°+30° = 60°.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним ⇒ ∠САD = ∠В + ∠С = 90° + 60° = 150°.
Ответ: 150°.
2-По теореме о пропорциональных отрезках прямоугольного треугольника:
СВ²=ДВ*АВ; АВ=СВ²:ДВ; АВ=10²:5; АВ=100:5; АВ=20.
АД=АВ-ДВ=20-5=15.
Ответ: 15.
В прямоугольном треугольнике АВС катет ВС, лежащий против угла 30°, равен половине гипотенузы АВ:
АВ=2*СВ=2*4=8
М - середина АВ, значит ВМ=АМ=4 и треугольник ВСМ - равнобедренный (ВС=ВМ=4)
В треугольнике АВС <B=180-<C-<A=180-90-30=60°
Поскольку ВСМ - равнобедренный, то углы ВСМ и ВМС при его основании равны:<BCM=<BMC=(180-<B):2=(180-60):2=60°
Все углы треугольника ВСМ по 60°, значит ВСМ - равносторонний, и СМ=4
В треугольнике АСМ:
СМ=АМ=4, он - равнобедренный, и MD - не только биссектриса, но и медиана тоже, значит точка D - середина АС.
Таким образом, MD - средняя линия треугольника АВС, поскольку соединяет середины сторон. Средняя линия параллельна ВС и равна половине этой стороны:
MD=1/2BC=1/2*4=2