Предмет: Математика,
автор: vosmoybgovno
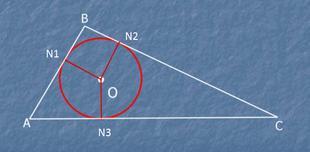
Окружность разделена тремя точками на части в отношении 17 : 12 : 7 и через эти точки проведены касательные к окружности. Найдите угол образовавшегося треугольника
vosmoybgovno:
с рисунком если можно
Ответы
Автор ответа:
4
Ответ:
Пошаговое объяснение:
Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами (или равен 180 - меньшая дуга, на которую опирается)
пусть дуги поделены так
тогда в градусах мы получим
теперь углы
(если рисунок не совсем точно отражает соотношения углов, не обессудьте, я просто эскизно рисовала)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: violaantonyuk
Предмет: Русский язык,
автор: gffffiii
Предмет: Русский язык,
автор: popova7
Предмет: Математика,
автор: нак31
Предмет: Математика,
автор: vikashvornikov