Question

Квадратное неравенство. Урок 3

Реши неравенство методом интервалов x(x – 3) ≤ 4 и определи количество целых решений.

Ответ:.

Назад

Проверить


​

Answer 1

Ответ:

[-1; 4]

6 целых решений.

Объяснение:

x(x - 3) ≤ 4

x² - 3x - 4 ≤ 0

Найдем нули функции у = х² - 3х - 4:

x² - 3x - 4 = 0

D = 3² + 4·4 = 9 + 16 = 25

√D = √25 = 5

$x_1=\dfrac{3-5}{2}=-1$

$x_2=\dfrac{3+5}{2}=4$

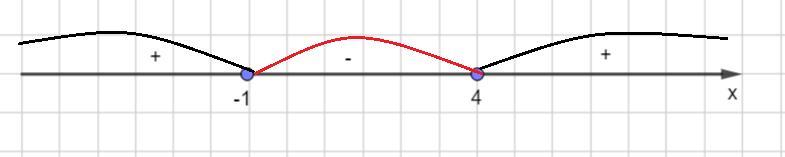
Отметим нули функции на числовой прямой и воспользуемся правилом чередования знаков (на правом интервале "+", далее знаки чередуются) см. рисунок.

у ≤ 0 при х ∈ [-1; 4], значит решением неравенства является промежуток [-1; 4].

Целые решения: - 1; 0; 1; 2; 3; 4, всего - 6 целых решений.

Answer 2

Ответ:

6.

Объяснение:

$x(x-3)\leq 4;\\x^{2} -3x\leq 4;\\x^{2} -3x-4\leq 0$

Рассмотрим функцию

$f(x)=x^{2} -3x-4$

Область определения функции

$D(f)=R$

Найдем нули функции, решив квадратное уравнение

$x^{2} -3x-4=0;\\D=(-3)^{2}-4\cdot1\cdot(-4)=9+16=25=5^{2}; \\\\x{_1}=\dfrac{3-5}{2} =\dfrac{-2}{2}=-1 ;\\\\x{_2}=\dfrac{3+5}{2} =\dfrac{8}{2}=4 .$

$(x+1)(x-4)\leq 0$

Нули функции разбивают область определения на три промежутка, на каждом из которых функция непрерывна, не обращается в нуль, а значит сохраняет свой постоянный знак.

Определим знак на каждом промежутке.

$f(x)\leq 0$  при   x∈ [-1;4]

Выпишем все целые решения : -1; 0; 1; 2; 3; 4.

Количество целых решений : 6.